فاجعه فرابنفش
ماکسول (1879-1831) نور را به صورت یک موج الکترومغناطیس در نظر گرفته بود. از اینرو ، همه فکر میکردند نور یک پدیده موجی است و ایده «مولکول نور» ، در اواخر قرن نوزدهم ، یک لطیفه اینترنتی یا SMS کاملاً بامزه و خلاقانه محسوب میشد. به هر حال ، دست سرنوشت یک علامت سؤال ناجور هم برای ماهیت موجی نور در آستین داشت که به «فاجعه فرابنفش» مشهور شد. یک محفظهی بسته و تخلیه شده را که روزنه کوچکی در دیواره آن وجود دارد، در کورهای با دمای یکنواخت قرار دهید و آنقدر صبر کنید تا آنکه تمام اجزاء به دمای یکسان (تعادل گرمایی) برسند. در دمای به اندازه کافی بالا ، نور مرئی از روزنه محفظه خارج میشود (مثل سرخ و سفید شدن آهن گداخته در آتش آهنگری).
جسم سیاه
نمودار انرژی تابشی در واحد حجم محفظه ، برحسب رابطه رایلی- جینز در فیزیک کلاسیک و رابطه پیشنهادی پلانک در تعادل گرمایی ، این محفظه دارای انرژی تابشی است که آن را در تعادل تابشی ـ گرمایی با دیوارهها نگه میدارد. به چنین محفظهای «جسم سیاه» میگوییم. یعنی اگر روزنه به اندازهی کافی کوچک باشد و پرتو نوری وارد محفظه شود، گیر میافتد و نمیتواند بیرون بیاید. فرض کنید میزان انرژی تابشی در واحد حجمِ محفظه (یا چگالی انرژی تابشی) در هر لحظه U باشد.
چه کسری از این انرژی تابشی که به شکل امواج نوری است، طول موجی بین 546 (طول موج نور زرد) تا 578 نانومتر (طول موج نور سبز) دارند؟ جواب فیزیک کلاسیک به این سؤال برای بعضی از طول موجها بسیار بزرگ است! یعنی در یک محفظهی روزنه دار که حتماً انرژی محدودی وجود دارد، مقدار انرژی در برخی طول موجها به سمت بی نهایت میرود. این حالت برای طول موجهای فرابنفش شدیدتر هم میشود.
فیزیک کوانتوم
دید کلی
نیلز بور (1962 - 1885) ، از بنیانگذاران فیزیک کوانتوم ، در مورد چیزی که بنیان گذارده است، جملهای دارد به این مضمون که اگر کسی بگوید فیزیک کوانتوم را فهمیده ، پس چیزی نفهمیده است. 
تقسیم ماده
از یک رشتهی دراز ماکارونی پخته شروع میکنیم. اگر این رشتهی ماکارونی را نصف کنیم، بعد نصف آن را هم نصف کنیم، بعد نصف نصف آن را هم نصف کنیم و ... شاید آخر سر به چیزی برسیم، البته اگر چیزی بماند! که به آن مولکولل ماکارونی میتوان گفت؛ یعنی کوچکترین جزئی که هنوز ماکارونی است. حال اگر تقسیم کردن را باز هم ادامه بدهیم، حاصل کار خواص ماکارونی را نخواهد داشت، بلکه ممکن است در اثر ادامه تقسیم ، به مولکولهای کربن یا هیدروژن یا ... بر بخوریم.
این وسط ، چیزی که به درد ما میخورد (یعنی به درد نفهمیدن کوانتوم!) این است که دست آخر ، به اجزای گسستهای به نام مولکول یا اتم میرسیم. این پرسش از ساختار ماده که آجرک ساختمانی ماده چیست؟ ، پرسشی قدیمی و البته بنیادی است. ما به آن ، به کمک فیزیک کلاسیک ، چنین پاسخ گفتهایم: ساختار ماده ، ذره ای و گسسته است؛ این یعنی نظریه مولکولی. تقسیم انرژی
ایدهی تقیسم کردن را در مورد چیزهای عجیبتری بکار ببریم، یا فکر کنیم که میتوان بکار برد یا نه. مثلا در مورد صدا. البته منظورم این نیست که داخل یک قوطی جیغ بکشیم و در آن را ببندیم و سعی کنیم جیغ خود را نصف ـ نصف بیرون بدهیم. صوت یک موج مکانیکی است که میتواند در جامدات ، مایعات و گازها منتشر شود. چشمههای صوت معمولا سیستمهای مرتعش هستند. ساده ترین این سیستمها ، تار مرتعش است که در حنجره انسان هم از آن استفاده شده است. براحتی و بر اساس مکانیک کلاسیک میتوان نشان داد که بسیاری از کمیتهای مربوط به یک تار کشیده مرتعش ، از جمله فرکانس ، انرژی ، توان و ... گسسته (کوانتیده) هستند.
گسسته بودن در مکانیک موجی پدیدهای آشنا و طبیعی است. امواج صوتی هم مثال دیگری از کمّیتهای گسسته (کوانتیده) در فیزیک کلاسیک هستند. مفهوم موج در مکانیک کوانتومی و فیزیک مدرن جایگاه بسیار ویژه و مهمی دارد و یکی از مفاهیم کلیدی در مکانیک کوانتوم است. پس گسسته بودن یک مفهوم کوانتومی نیست. این تصور که فیزیک کوانتومی مساوی است با گسسته شدن کمّیتهای فیزیکی ، همه مفهوم کوانتوم را در بر ندارد؛ کمّیتهای گسسته در فیزیک کلاسیک هم وجود دارند. بنابراین ، هنوز با ایده تقسیم کردن و سعی برای تقسیم کردن چیزها میتوانیم لذت ببریم! 
مولکول نور
فرض کنید بجای رشتهی ماکارونی ، بخواهیم یک باریکه نور را بطور مداوم تقسیم کنیم. آیا فکر میکنید که دست آخر به چیزی مثل «مولکول نور» (یا آنچه امروز فوتون مینامیم) برسیم؟ چشمههای نور معمولاً از جنس ماده هستند. یعنی تقریباً همه نورهایی که دور و بر ما هستند از ماده تابش میکنند. ماده هم که ساختار ذرهای ـ اتمی دارد. بنابراین ، باید ببینیم اتمها چگونه تابش میکنند یا میتوانند تابش کنند؟ تابش الکترون
در سال 1911، رادرفورد (947-1871) نشان داد که اتمها ، مثل میوهها ، دارای هسته مرکزی هستند. هسته بار مثبت دارد و الکترونها به دور هسته میچرخند. اما الکترونهای در حال چرخش ، شتاب دارند و بر مبنای اصول الکترومغناطیس ، «ذره بادارِ شتابدار باید تابش کند» و در نتیجه انرژی از دست بدهد و در یک مدار مارپیچی به سمت هسته سقوط کند. این سرنوشتی بود که مکانیک کلاسیک برای تمام الکترونها پیش بینی میکند. طیف تابشی اتمها ، بر خلاف فرضیات فیزیک کلاسیک گسسته است. به عبارت دیگر ، نوارهایی روشن و تاریک در طیف تابشی دیده میشوند.
اگر الکترونها به این توصیه عمل میکردند، همه مواد (از جمله ما انسانها) باید از خود اشعه تابش میکردند (و همانطور که میدانید اشعه برای سلامتی بسیار خطرناک است)، ولی میبینیم از تابشی که باید با حرکت مارپیچی الکترون به دور هسته حاصل شود اثری نیست و طیف نوری تابش شده از اتمها بجای اینکه در اثر حرکت مارپیچی و سقوط الکترون پیوسته باشد، یک طیف خطی گسسته است؛ مثل برچسبهای رمزینهای (barcode) که روی اجناس فروشگاهها میزنند.
یعنی یک اتم خاص ، نه تنها در اثر تابش فرو نمیریزد، بلکه نوری هم که از خود تابش میکند، رنگهای یا فرکانسهای گسسته و معینی دارد. گسسته بودن طیف تابشی اتمها از جمله علامت سؤالهای ناجور در مقابل فیزیک کلاسیک و فیزیکدانان دههی 1890 بود.
واحد مناسب
همه ی ما می دانیم در این جهان کمیت های فراوانی وجود دارد. کمیت ها به دو دسته مهم تبدیل می شوند. 1.کمیت های اصلی 2.کمیت های فرعی کمیت های اصلی به کمیت هایی گفته می شود که از طریق کمیت های دیگر نتوان آن را اندازه گیری کرد. کمیت های فرعی به کمیت هایی گفته می شود که بتوان آن ها را از طریق کمیت های دیگر و از راه ضرب و تقسیم و... آن ها را پیدا کرد. کمیت های اصلی مانند: طول و جرم و زمان و دما و ... کمیت های فرعی مانند:مساحت و حجم و وزن و... کمیت ها را به وسیله واحد و وسیله اندازه گیری می توان اندازه گیری کرد پس واحد آن باید در دسترس همه مردم باشد و دیگر آن که اندازه آن تغییر نکند و در همی جا به یک اندازه باشد. به این واحد استاندارد (si) می گویند. پس هر واحدی واحد مناسب برای اندازه گیری نیست. واحد های نامناسب:ذراع و وجب و طول وجب پادشاه!!!! و...
تعریف فیزیک
فیزیک را دانش کشف و استفاده علمی از روابط و قوانین حاکم بر پدیده های طبیعی می نامند که مبنای آن بر تجربه و آزمایش است.
فیزیک
یکی از کمیت های دیگر جرم است. جرم به مقدار ماده ی تشکیل دهنده جسم می گویند.
هواژل سبک ترین در جهان
بیشتر یا بهتر بگم همه ی کسانی که هواژل (aerojel) رو برای اولین بار می بینند ، هواژل در حالی که بیشتر از هوا تشکیل شده ( 90% تا 99.8% ) جامد شفافی است که برای گرما و صوت هم عایق بسیار خوبی است ؛ چگالی آن تا 5 میلی گرم بر سانتی متر مکعب است ، یعنی حدود سه برابر چگالی هوا . با اینکه هواژل ساختاری متخلخل دارد ، اما بر خلاف سایر مواد متخلخل که کدرند ، هواژل بسیار شفاف می باشد و می توان از پشت آن اجسام را مشاهده نمود ! به علت ساختار متخلخل دارای مساحتی بسیار زیاد ، برای مثال یک تکه ی 28.35 گرمی از هواژل مساحتی خارجی به اندازه ی نزدیک به مساحت شش زمین فوتبال دارد . ( راستی رفتن ایران به جام جهانی رو هم تبریک می گم ! ) هواژل سیلیسی عمده ترین هواژل ساخته شده می باشد ، ولی آن را از بسیاری از اکسید های فلزی نیز مانند : آهن ، قلع ، آلومین ، اکسید تیتانیم و اکسید زیرکونیم و ... می توان تهیه کرد . در 20 سال گذشته کاربرد هایی گوناگونی برای این ماده ی جالب پیشنهاد شده : 1 . در تولید پنجره های ابر نا رسانا . 2 . به عنوان محافظ برای باتری ها ی خورشید ی . 3 . عایق برای تأسیسات حرارتی . 4 . شیشه ، آینه و همنچنین عدسی های سبک و شفاف ( در دوربین ها و ... ) . و اما هواژل چگونه ساخته می شود ؟ به طور خیلی مختصر توضیح می دم . حتماً دیدید که اگر یک ماده ی ژل مانند. مانند ژله های خوردنی اگر در محیط بمانند ، پس از مدتی حجمشان کم می شود ؛ (البته منظورم خوردنشون نیست ! ) به علت تبخیر شدن مقدار کمی از آب آن ها . اما با این روش ( یعنی خشک کردن تدریجی آب آنها ) نمی توان هواژل تهیه کرد ؛ چون همراه با تبخیر شدن آب ساختار ژل به هم می ریزد ، علت این امر نیروی کشش سطحی خیلی زیاد آب است ، پس باید به طریقی آب رو از ساختار ژل خارج نمود بدون اینکه به ساختار آن صدمه ای وارد شود . خوب این کار رو با افزایش فشار محیط آزمایشگاهی انجام دادند . ساموئل کیستلر ( samuel kistler ) کاشف هواژل ابتدا این ایده به ذهنش رسید ؛ چون فشار های بیشتر از فشار بخار مایع ، باعث می شودتا مایع در فشار بحرانی خود به گاز تبدیل شود. اما قبل از تبدیل آب فوق بحرانی به گاز ( آب با دمای بیشتر از 100ْ و فشار بیشتر از 1 atm ( آتمسفر ) آب ساختار ژل را ( که در آزمایش کیستلر سیلیسی بود .) در خود حل می کرد . پس دانشمند قصه ی ما مجبور شد تا آب درون ژل را با یک مایع دیگر تعویض کند ، که مشکلات آب را ( حل کردن سیلس درون خود را در شرایط فوق بحرانی ) نداشته باشد . به این صورت بود که نخستسن هواژل توسط ساموئل کیستلر ساخته شد . برای اینکه سرعت بار گذاری weblog کم نشه بقیه ی عکس ها رو در ادامه ی مطلب می ذارم . در آخر ایندفه آمریکا بازی خیلی بدی رو شروع کرد . خیلی روشنه که انفجار حرم دو امام بزرگ شیعیان کار امریکا و همپیمانش انگلیسه . این فاجعه ی بزرگ رو هم به امام عصرمون تسلیت میگم . به امید روز های بهتر . انشاالله .بی برو برگرد جا می خورند . ظاهری شبه گونه و ابر مانند ، هواژل را مثل داستان های علمی تخیلی جذاب می کنه .
چرا باید ریاضی بخوانیم
چرا باید ریاضیات بخوانیم؟ (ولادیمر ارنولد)
چرا باید ریاضیات بخوانیم؟راجر بیکن فیلسوف انگلیسی در سال 1267 میلادی پاسخ این سوال را چنین داده است:
(کسی این کار را نکند نمیتواند چیزی از بقیه علوم و هر آنچه دراین جهان است بفهمد...چیزی که بدتر است این است که کسانی که ریاضیات نمیدانند به جهالت خودشان پی نمی برند ودر نتیجه در پی چاره جویی بر نمی آیند.))
می توانم همین جا سخنرانیم را پایان دهم اما ممکن است بعضیها فکر کنند که شاید خیلی چیزها در هفت قرن گذشته تغییر کرده باشد....
شاهدی تازه تر می آورم پال دیراک از خالقان مکانیک کوانتومی معتقد است که وقتی تئوری فیزیکی ای را پایه ریزی می کنید نبایدبه هیچ شهود فیزیکی ای اعتماد کنید.پس به چه چیزی اعتماد کنید؟به گفته ی این فیزیکدان مشهور فقط به برنامه ای متکی بر ریاضیات _ولو اینکه در نگاه اول ربطی به فیزیک نداشته باشد.
در حقیقت در فیزیک تمامی ایده های صرفا فیزیکی رایج در ابتدای این قرن را کنار گذاشته اند در حالی که الگوهای ریاضی ای که به زرادخانه فیزیکدان ها راه یافته اند به تدریج معنای فیزیکی یافته اند.در اینجاستکه قابل اعتماد بودن ریاضیات به روشنی رخ مینمایاند.
بنابراین الگوسازی ریاضی روشی پربار برای شناخت در علوم طبیعی است.اکنون می خواهیم الگوهای ریاضی را از نگاهی دیگر یعنی مسئله ی آموزش ریاضی بررسی کنیم.
سه روش اموزش ریاضیات
در اموزش ریاضیات روسی (هم در دبیرستان و هم در مقاطع بالاتر) ما پیرو نظام اموزشی اروپایی هستیم که بر اساس ((بورباکی ای سازی))ریاضیات بنا شده است (نیکلاس بورباکی نام مستعار گروهی از ریاضیدانان فرانسوی است که ازسال 1939 به انتشار مجموعه ای از کتابها دست زده اندکه در انها شاخه های اصلی ریاضیات جدید به طور اصولی_یعنی به روش اصل موضوعی براساس نظریه ی مجموعه ها_شرح داده شده است.)
اصولی کردن ریاضیات به نوعی تصنعی کردن آموزش آن منجر می شود واین زیانی است که بورباکی ای سازی به آموزش ریاضیات وارد کرده است.نمونه ای شگرف مثال زیر است:
از دانش آموز سال_دومی مدرسه ای در فرانسه پرسیده اند ((دو بعلاوه ی سه چقدر میشود؟)) پاسخ چنین بود ((چون جمع تعویض پذیر است می شود سه بعلاوه ی دو.))
پاسخی واقعا قابل تامل! کاملا درست است اما دانش آموزان حتی به جمع کردن ساده ی این دو عدد هم فکر نکرده اند زیرا در تعلیم انها تکیه بر ویژگی های عملها بوده است. در اروپا معلمان متوجه نارساییهای این روش شده اند و بورباکی ای سازی را کنار گذاشته اند.
طی چند سال گذشته آموزش ریاضیات روسی دستخوش تغییراتی به سبک آمریکایی شده است.اساس این سبک این اصل است: آنچه را که برای کاربردهای عملی لازم است آموزش بدهید.در نتیجه کسی که فکر می کند به ریاضیات احتیاجی نخواهد داشت اصلآ لازم نیست ان را بخواند.ریاضیات درسی اختیاری در دوره ی راهنمایی و دبیرستان است_مثلآ یک سوم دانش آموزان دبیرستانی جبر نمی خوانند.نتیجه ی این امر را در مثال زیر روشن کرده ایم:
در آزمونی برای دانش آموزان چهارده ساله ی آمریکایی از آنها خواسته شده بود که برآورد کنند (نه اینکه حساب کنند بلکه برآورد کنند) که اگر 80 درصد از عدد 120 رابرداریم این عدد چه تغییری می کند.سه نوع پاسخ را می توانستند انتخاب کنند: زیاد میشود،تغییری نمیکند،کمتر میشود.تقریبآ 30 درصد دانش آموزان سوال شونده پاسخ درست را برگزیده بودند.یعنی اینکه پاسخها را تصادفی انتخاب کرده بودند.نتیجه: هیچ کس هیچ چیز نمی داند.دومین ویژگی شاخص روش آموزش ریاضی آمریکایی،کامپیوتری کردن آن است.
جذابییت کار با کامپیوتر به خودی خود به گسترش تواناییهای فکری کمکی نمی کند.مثالی دیگر از یکی از آزمونهای آمریکا میاوریم:
کلاسی 26 دانش آموز دارد.این دانش آموزان می خواهند با اتومبیل به مسافرت بروند.در هر اتومبیل یک نفر از اولیا و چهار دانش آموزجا می شوند.چند نفر از اولیا را میتوانیم دعوت کنیم؟
جوابی که همه داده بودند 65 نفر بود جواب کامپیوتر :
است،ودانش آموزان می دانستند که اگر جواب باید عددی صحیح باشد،می توان بلایی سر ممیز آورد_مثلآ می توان اصلآ آن را برداشت.
نمونه ی دیگری از یکی از آزمونهای رسمی دانش آموزی در سال 1992 می آوریم:
رابطه ی کدام زوج شباهت بیشتری به رابطه ی میان زاویه و درجه دارد:
الف) زمان وساعت
ب) شیر وکوارت ((واحد اندازه گیری مایعات برابر با 44/1 لیتر))
ج) مساحت و اینچ مربع
پاسخ،مساحت و اینچ مربع است،زیرا درجه ی کوچکترین واحد اندازه گیری زاویه و اینچ مربع کوچکترین واحد اندازه گیری مساحت است،اما ساعت را می توان به دقیقه هم تقسیم کرد.
طراح این مسئله مسلمآ مطابق نظام امریکایی می اندیشیده است.می ترسم که طولی نکشد که ما هم به چنین سطح نازلی برسیم.( جو برمن،استاد ریاضی در نیویورک توضیح داده که( از نظر او که آمریکایی است) ،پاسخ درست این مسئله کاملآ روشن است.او گفت که ((اصل مطلب این است که من می توانم میزان حماقت طراح این مسئله را دقیقآ تصور کنم.))_) مایه ی شگفتی است که تعداد زیادی ریاضیدان و فیزیکدان برجسته در ایالات متحده وجود دارد.
امروزه آموزش ریاضیات ما آرام آرام از نظام اروپایی به نظام آمریکایی تبدیل می شود.مطابق معمول ،باز هم عقبیم،حدود سی سال از اروپا عقبتریم و بنابراین سی سال بعد زمان آن فرا میرسد که اوضاع را سروسامان بدهیم و از چاهی که با ظناب نظام آموزشی آمریکایی به آن رفته ایم بیرون بیاییم.
سطح آموزش ریاضی سنتی ما بسیار بالا و بر اساس آموزش مسئله های حساب بوده است.حتی تا همین بیست سال پیش هم خانواده هایی بودند که نسخه هایی از کتابهای قدیمی مربوط به مسئله های ((سود و زیان)) را داشتند.در حال حاضر، همه ی اینها از بین رفته است.در آخرین اصلاحات آموزش ریاضی،جبری سازی، دانش آموزان را به روبات تبدیل کرده است.
مساله های حساب است که ((بی محتوایی)) ریاضیاتی را که تدریس می کنیم نشان می دهند مثلآ این مسئله را در نظر بگیرید:
1.سه تا سیب داریم.یکی را برمی داریم.چند تا باقی مانده است؟
2.چند برش با اره لازم است تا تکه ای هیزم را به سه بخش تقسیم کنیم؟
3.تعداد خواهران بوریس از تعداد برادرانش بیشتر است.در خانواده ی او تعداد دختران چند تا بیشتر از تعداد پسران است؟
از منظر حساب اینها مساله های متفاوتی هستند،زیرا محتوایشان فرق می کند.همچنین،تلاش فکری لازم برای حل کردن مسئله ها هم کاملآ متفاوت است،هر چند که الگوی جبری هر یک از آنها یکی است: 2=1-3 جالب توجه ترین نکته در ریاضیات،فراگیر بودن شگفت آور الگوها و کارایی نامحدود انها در مساله های علمی است.
به قول ولادیمیر مایاکوفسکی،شاعر بزرگ روس: ((کسی که اولین بار دو بعلاوه ی دو می شود چهار را، مطرح کرده است حتی اگر با جمع کردن دو تا ته سیگار با دو تا ته سیگار دیگر به این حقیقت رسیده باشد،ریاضیدان بزرگی بوده است.هر کس پس از او به این نتیجه رسیده باشد،حتی اگر چیزهای بسیار بزرگتری،مثل لوکوموتیوها را با هم جمع کرده باشد،ریاضیدان نیست)) لوکوموتیو شماری،روش آمریکایی آموزش ریاضیات است.چنین چیزی مصیبت بار است.طرز پیشرفت فیزیک در ابتدای سال اخیر نمونه ای است که نشان می دهد ریاضیات لوکوموتیوی به مراتب از ریاضیات ته سیگاری به درد نخورتر است:ریاضیات کاربردی نتوانسته همگام با فیزیک پیشترفت کند،در حالی که ریاضیات نظری هر آنچه را که فیزیکدانان برای بسط بیشتر دانش خودشان نیاز داشته اند برایشان فراهم کرده است.ریاضیات لوکوموتیوی از روال معمول عقب می ماند: تا حساب کردن با چرتکه را آموزش بدهیم،سر و کله ی کامپیوترها پیدا می شود .باید شیوه ی فکر کردن را آموزش بدهیم،نه طرز فشار دادن دکمه ها را.
اشکانیان
برنهادهی بنیادین «ناصر پورپیرار» در کتاب سراسر نامفهوم و مهملاش به نام «اشکانیان» آن است که "اشکانیان" نه صاحبان ایرانیتبار یک امپراتوری نیرومند و یکپارچه، بل که یونانیانی بودند که در سال 146 پ.م. با تسلط روم بر آتن، به ایران گریخته و مهاجرت کردند و در این کشور مهاجرنشینهای پراکندهای را برپا نمودند و سرانجام با تضعیف قدرت روم، در 214 میلادی، اقامتگاههای خود را در ایران وانهاده و به یونان بازگشتند!! خواننده در وهلهی نخست انتظار دارد که نویسنده، اسناد و مدارک صریح و دقیق ادعای انقلابی خود را دربارهی گریز و مهاجرت گستردهی یونانیان به ایران در پی اشغال آتن به دست رومیان، و سپس بازگشت آنان را از ایران به آتیک پس از برافتادن سلطهی روم، جزء به جزء عرضه کند. اما پورپیرار که گویی با بیان این مهملات در حال قصهگویی برای نوههای خویش است، هیچ سراغ و نشانی را از چنان اسنادی در اختیار ندارد و به خوانندگان ارائه نمیکند. بدین سان، پورپیرار، این ادعای وقیح و موهوم خود را در همان ابتدا به سبب عدم همراهی با هر گونه سند و مدرکی، به دست خویش ابطال میکند.از آن جا پورپیرار در برخورداری از سند و مدرک - بل که عقلانیت - دچار تهیدستی و فقر کامل است، برای اثبات ادعاهای خود به دلایلی نامربوط و گمراهگرانه متوسل میشود و میگوید که چون سبک هنر و معماری عصر اشکانی و زبان رایج در آن یونانی بود، پس "اشکانیان" یونانیتبار بودهاند!!! اما پورپیرار کاملاً غافل است که هنر و معماری هخامنشیان (یا به قول او، اسلاوهای یهودی!) به شیوهی «اکدی- ایلامی» بود و زبان رسمی آنان نیز ایلامی- آرامی. حتا از دوران پس از اسلام نیز میتوان نمونه آورد و گفت که هنر و معماری غزنویان و سلجوقیان و ایلخانان نه به سبک چادرنشینان بیابانگرد دشتهای مغولستان، و زبان رسمی آنان نه ترکی، بل که این همه یکسره ایرانی بود. بنابراین استفادهی اشکانیان از شیوهها و زبان یونانی که از زمان اسکندر در ایران حاکم گردیده و به ویژه در میان طبقات فرادست و وابسته به دربار مقدونی، مُد و مرسوم بود، امری کاملاً طبیعی و عادی و مطلقاً فاقد آن معنایی است که پورپیرار با مسخرهبازیهایش از آن برداشت و القا میکند. پورپیرار در جایی دیگر از کتاب خود، گویی که قصد تمسخر همهی ادعاهای مهمل خود را دارد، نخست مدعی میشود که نام "ارشک" و دیگر شاهان اشکانی، یونانی است. اما بعد به ناگزیر اعتراف میکند کهدر هیچ واژهنامهی یونانیای، چنین واژگانی نیامده و معنا نشده است!! او که در نهایت همهی رشتههای خود را پنبه شده مییابد، به همان دستاویز سخیف و کودکانهی همیشگیاش متوسل میشود و میگوید که همهی واژهنامههای یونانی موجود قلابی و جعلیاند و نامهای یاد شده عمداً و برای پنهان کردن ماهیت یونانی اشکانیان، به دست توطئهگران یهودی از این کتابها حذف شدهاند!!! هذیانگوییهای مالیخولیایی پورپیرار پایانناپذیر است.
پورپیرار که از جعل و جاسازی دروغ در جعبهی تاریخ ابایی ندارد و با تناقضگوییهای پیاپی، ادعاهایش را به دست خویش ابطال میکند، گواهی انبوهی از نویسندگان کهن یونانی و لاتینی و ارمنی (پلوتارک، استرابو، آرین، هرودیان، موسا خورنی و…) را دربارهی وجود یک امپراتوری نیرومند و یکپارچه و ایرانی به نام اشکانی (یا پارتی) مردود میشمارد و این همه را ساختگی و جعلی توصیف میکند. اما چند صفحه بعد، آن جا که «اسکندر» را رهاننده و آزادیبخش اقوام شرق میانه از شرّ هخامنشیان (!) میخواند و حاکمیت اسکندر و سلوکیان را بر ایران تقدیس و تحسین میکند، اصالت و صحت همان منابع کهن یونانی و لاتینی و ارمنی را تأیید میکند چرا که تنها همین مراجع هستند که از اسکندر مقدونی و لشکرکشی وی به ایران و جانشینان سلوکی وی سخن راندهاند و آگاهیهای کنونی ما در این زمینهی کاملاً وابسته به همین منابع است. بدین ترتیب، پورپیرار آن جا که منافعاش اقتضا میکند، اصالت و صحت منابع یاد شده را تأیید میکند و آن جا که منافعاش اقتضا نمیکند، همانها را فوراً و بدون توجه به برملایی تناقضگوییاش، مردود میشمارد. آیا ممکن است نویسندهای تا این حد خوانندهاش را تحقیر کند و او را در جای کودنی فاقد تفکر بنشاند، قدرت تعقل و تمییز را از او سلب شده بیانگارد و این همه سخن ضد و نقیض بیسند و محتوا را در مقابل او انبار کند؟
شخص پانترکیستی به نام «رهگذر» (که در وبلاگ پورپیرار گفته بود مغها همان مغولها هستند!!) به پیروی از آموزگار ضدایرانیاش، نوشته بود که نسخهی اصلی هیچ یک از آثار کهن تاریخی یونانی و لاتینی در دست نیست، بنابراین همهی این منابع جعلیاند!! در پاسخ به شبههافکنی مهمل و نامربوط این فرد باید بگویم که ما هیچ نسخهی اصلی و اصیلی - مثلاً - از دیوان حافظ، مثنوی معنوی یا تاریخ بیهقی نداریم. اما به نسخههایی از این کتابها که حتا صدها سال پس از عصر نویسندگانشان کتابت شدهاند، اعتماد میکنیم و آنها را مقبول میدانیم و ادعا نمیکنیم که فرضاً، هیچ گاه دیوان حافظی وجود نداشته است. به همین سان، از قرآن نیز هیچ نسخهی اصل و اصیلی در دست نداریم اما با این حال، کسی موجودیت و اصالت قرآن کنونی را انکار نمیکند. از تاریخ هردوت نیز تاکنون نسخهای که به خط او باشد یا در عصر او نوشته شده باشد در دست نیست اما حتا پورپیرار هم به اصالت آن صحه میگذارد! در اعصار کهن، هیچ سازمان یا نظام خاصی برای حفظ و نگهداری آثار محدود مکتوب وجود نداشت و به لحاظ محدودیت در نشر و تکثیر کتب، چه بسا با مفقود شدن یا نابود شدن یک جلد کتاب، هرگز نسخهی دیگری برای جبران فقدان آن یافته نمیشد. به هر حال، غالب کتابهای کهن موجود - چه در ایران و چه در غیر آن - نه مبتنی بر نسخههایی اصیل و به خط خود نویسندگانشان، بل که متکی به رونوشتهایی بسیار متأخرند که معمولاً امانتدارانه، استنساخ شده و نسل به نسل منتقل گشته و دست به دست، گردیدهاند. بنابراین، هرگز نمیتوان ادعا کرد که به سبب در دست نبودن نسخهی اصلی فلان کتاب، آن کتاب جعلی و دروغین است.
استقرا
منبع : سایت رشد استقرا
مقدمه
برای درک مفهوم استقرا به مراحل اثبات یکی از برابریهای ساده در ریاضیات توجه کنید:
مجموع اعداد طبیعی زیر را در نظر بگیرید: 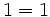

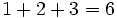
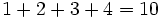

اگر به طور که بخواهیم 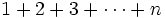 را بدست بیاوریم یک راه این است که الگویی از مجموع اعداد بالا بدست آورده و سعی در اثبات آن نمائیم.
را بدست بیاوریم یک راه این است که الگویی از مجموع اعداد بالا بدست آورده و سعی در اثبات آن نمائیم. 
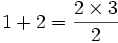
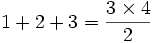

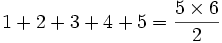
و به این ترتیب الگوی 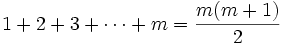 را برای مجموعة فوق در نظر میگیریم.
را برای مجموعة فوق در نظر میگیریم.
این الگو در حقیقت یک گزاره بر روی اعداد طبیعی میباشد که میتوان آن را با  به معنی
به معنی  نمایش داد.
نمایش داد.
اگر چه اثبات این الگو به طور مستقیم و بدون کمک به استقرا به سادگی ممکن میباشد ولی در حل مسائل ریاضی به دفعات به حدسهایی برمیخوریم که اثبات آنها میتواند مشکل باشد در ایدة استقرا یکی از زیباترین ایدههای موجود برای کمک به ما میباشد.
برای آنکه بیشتر آمادگی ذهنی برای درک استقرا پیدا کنیم به همان مثال مجموع اعداد 1 تا  میرویم، و میخواهیم گزارة
میرویم، و میخواهیم گزارة  را که گزارهای دربارة عدد
را که گزارهای دربارة عدد  میباشد ثابت کنیم.
میباشد ثابت کنیم.
در ایدة استقرا که جلوتر به تعریف دقیق آن میپردازیم نخست باید برای  های کوچک درستی
های کوچک درستی  را نشان دهیم مانند:
را نشان دهیم مانند: 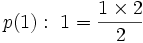
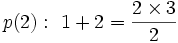
حال میدانیم لااقل برای تعدادی از ابتدای اعداد طبیعی  درست است. اکنون با فرض آنکه برای
درست است. اکنون با فرض آنکه برای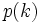 حکم درست باشد، درستی
حکم درست باشد، درستی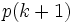 را نتیجه میگیریم (دقت کنید درستی
را نتیجه میگیریم (دقت کنید درستی 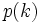 را فرض میکنیم.
را فرض میکنیم. 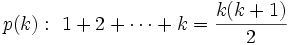

خوب حال شما بگوئید ما برای چند عدد طبیعی کوچکترین درستی را ثابت کرده و با فرض درستی
را ثابت کرده و با فرض درستی 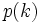 درستی
درستی 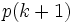 را ثابت کردیم، با این حساب آیا میتوان گفت که
را ثابت کردیم، با این حساب آیا میتوان گفت که برای تمامی اعداد طبیعی برقرار است؟ !
برای تمامی اعداد طبیعی برقرار است؟ !
به موضوع بالا فکر کنید چون اگر چه بعداً توضیح داده میشود ولی اگر اکنون آن را برای خود تجزیه و تحلیل کنید برای درک مطالب آینده راحتتر خواهید بود. چند نماد پرکاربرد
نماد مجموع  : از این جا به بعد با مجموع پشت سرهم دنبالهای از اعداد سروکار خواهیم داشت. برای نشان دادن مجموع
: از این جا به بعد با مجموع پشت سرهم دنبالهای از اعداد سروکار خواهیم داشت. برای نشان دادن مجموع  از نماد
از نماد 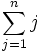 استفاده میکنیم، و این نماد یعنی تابع
استفاده میکنیم، و این نماد یعنی تابع 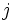 از حداقل مقدار 1 شروع شده و تا حداکثر
از حداقل مقدار 1 شروع شده و تا حداکثر  میرود و حاصل تمام مقادیر با هم جمع میشود. به طور کلی چند نمونه پرکاربرد:
میرود و حاصل تمام مقادیر با هم جمع میشود. به طور کلی چند نمونه پرکاربرد: 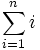 به جای
به جای 
 به جای
به جای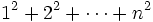
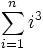 به جای
به جای 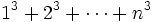
و به همین ترتیب …
و به طور کلی
از 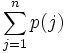 به جای
به جای 
استفاده میشود.
دقت کنید در نماد 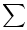 که آن را سیگما بخوانید سه قسمت مهم وجود دارد که در شکل قبل نشان داده شده است.
که آن را سیگما بخوانید سه قسمت مهم وجود دارد که در شکل قبل نشان داده شده است. قضیه .
میتوان سیگمای مجموع دو تابع یعنی 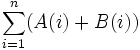 را به صورت مجموع دو سیگما هر یک از توابع یعنی
را به صورت مجموع دو سیگما هر یک از توابع یعنی 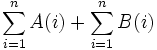 نوشت.
نوشت. قضیه .
 که k عددی ثابت است.
که k عددی ثابت است.
دو قضیه بالا به راحتی قابل اثبات بوده و از اثبات آنها صرفنظر میکنیم.
">نماد حاصلضرب
به طریق مشابه برای حاصلضرب 
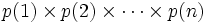 داریم:
داریم: 
به عنوان نمونه:  به جای
به جای 
 به جای
به جای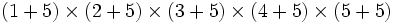 .
.
