هندسه اقلیدسی

اقلیدس ریاضیدان یونانی،پسر نوقطرس بن برنیقس،ریاضیدان و منجم بزرگ تاریخ علم،به سال 323 ق.م متولد شد،وی از تبار فنیقی و نخستین رئیس بخش ریاضیات بود، در زبان یونانی اقلی به معنی کلید و دس به معنای هندسه و اقلیدس به معنای کلید هندسه است،در آن زمان مرگ اسکندر فرا رسید و سردارانش برای کسب قدرت با یکدیگر جنگیدند. بطلمیوس یکی از سرداران اسکندر بود که مصر را گرفت و در آن جا تشکیل حکومت داد. وی از علم و دانش حمایت می کرد و دانشمندان و دوستداران علم و دانش را دعوت می کرد تا در اسکندریه اقامت کنند.
اقلیدس بیش از 30 سال نداشت که به خواهش و درخواست بطلمیوس برای تدریس به اسکندریه رفت و در این شهر مکتب فلسفی خود را پایه گذاری کرد. اقلیدس مردی محبوب، آرام، فروتن و نیکوکار بود و در حضور مستبدان و سرداران زورگو در نهایت صراحت صحبت می کرد. بطلمیوس فرمانروای مصر هنگامی که خواست هندسه را بیاموزد آن را دشوار دید و ترجیح داد که از راه ساده تری به فهم آن موفق شود، بنابر این از اقلیدس پرسید: آیا امکان دارد قضایا را به نحو ساده تری بیان کرد؟ اقلیدس به وی جواب داد: غیر ممکن است، در هندسه راه مخصوص شاهانه وجود ندارد!
وی به مادیات اهمیت چندانی نمی داد.زمانی که شاگردی از وی پرسید که از هندسه چه نفعی می بریم؟در پاسخ به وی رو به غلامی کرد و گفت که به شاگردش یک اوبولوس بدهد زیرا که وی می خواهد از آنچه که می خواند بهره ببرد.وی بسیار متواضع و مهربان بود.
در حدود 300 ق.م ،اقلیدس مدرسه ای را در اسکندریه بنا می کند که به مرکز مطالعات علمی یونان مبدل می گردد.
 کتاب مقدمات اقلیدس یا کتاب هندسه که سه قرن قبل از میلاد به نگارش در آمده، به زبان های مختلف دنیا ترجمه شده است و از آن زمان که فن چاپ مرسوم شد تا به حال بیش از2000 بار چاپ گردیده است.زمانیکه این کتاب منتشر شد، چنان نویسنده اش را مشهور کرد که تا20 قرن بعد هرگونه تغییر در آن به معنی توهین به مقدسات عالم محسوب می شد. تامدتها مردم بر این تصور بودند که اصل موضوع های اقلیدس هیچ گاه قابل تغییر نیست و تغییر در آن صورت نمی گیرد، اما دانشمندان برجسته ای چون ریمان لباچفسکی، علم ریاضیات را توسعه دادند و هندسه هایی غیراقلیدسی ارائه کردند.اقلیدس نابغه برجسته ای بود که ذوق سرشاری در زمینه تدوین داشت و این مطلب را می توان با مطالعه کتاب (نور) به خوبی متوجه شد.
قرن‌ پنجم‌ شاهد اوج‌ قدرت‌ ادبی‌ یونان‌، قرن‌ چهارم شاهد شکوفایی‌ فلسفه‌ و قرن‌ سوم‌ شاهد تکامل‌ علوم‌ بود. سلاطین‌ بیش‌ از دموکراسیها نسبت‌ به‌ تحقیقات‌ علمی‌ گذشت‌ و مساعدت‌ روا می‌داشتند. اسکندر کاروانهایی‌ مرکب‌ از جدولهای‌ نجومی‌ بابلی‌ به‌ شهرهای‌ یونانی‌ سواحل‌ آسیا فرستاد که‌ به‌ زودی‌ به‌ زبان‌ یونانی‌ ترجمه‌ شدند. بطالسه‌ موزه‌ی‌ مطالعات عالی‌ را بر پا داشتند و علوم‌ و ادبیات‌ فرهنگهای‌ مدیترانه‌ای‌ را در کتابخانه‌ی‌ کتابخانه‌ی بزرگ‌ خود متمرکز کردند. بطالسه‌ موزه‌ی‌ مطالعات عالی‌ را بر پا داشتند. آپولونیوس‌ مقاطع‌ مخروطی‌ خود را به‌ آتالوس‌ اول‌ هدیه کرد،‌و ارشمیدس‌ تحت‌ حمایت‌ هیرون‌ دوم‌ به‌ تعیین‌ نسبت‌ محیط‌ دایره‌ به‌ قطر آن‌ و محاسبه‌ی‌ تعداد ماسه‌هایی‌ که‌ برای‌ پر کردن‌ جهان‌ لازم‌ است‌ پرداخت.
با وجود تمامی اینها،موفقترین علم نزد آن زمان هندسه بود.اقلیدس متعلق به این دوره می باشد.حدود 2000 سال است که  اقلیدس با علم هندسه یاد می کنیم.ارشمیدس از دانشمندان باستان نیز دورانی را در نزد شاگردان اقلیدس به تحصیل علم پرداخت و به ریاضیات اشتیاق فراوانی یافت.

آثار اقلیدس:
اقلیدس مجموعه ای از 13 کتاب را به نام اصول تالیف می کند(کتابهای‌ اول‌ و دوم‌ خلاصه‌ای‌ از کارهای‌ فیثاغورس‌ در هندسه‌ به‌ دست‌ می‌دهند، کتاب‌ سوم‌ کارهای‌ بقراط‌ خیوسی،کتاب‌ پنجم‌ کارهای‌ ائودوکسوس، کتابهای‌ چهارم، ششم‌ و یازدهم‌ و دوازدهم‌ کارهای‌ فبثاغورسیان‌ متأخر و دانشمندان‌ هندسه‌ی یونانی،‌ کتابهای‌ هفتم‌ تا دهم‌ از ریاضیات‌ عالی‌ بحث‌ می‌کنند.)،این کتابها همچنین زیر بنای ریاضیات جدید را پی می نهند.
 که مهمترین کتاب او می باشد و به عربی ترجمه شده و در سراسر اروپا و خاور میانه گسترش یافت . کتاب اصول وی در زمینه هندسی یونانی ، جبر و نظریه اعداد نوشته شده است . که شامل 13 مقاله و 465 قضیه می باشد و در زمینه دایره ، خط راست ، هندسه فضایی  صفحه و کره ، اشکال منتظم ، اعداد گنگ ، استفاده از خط کش و پرگار در ترسیمات و ..... می باشد که البته اقلیدس مطالب و نظریه های جدید عنوان نکرده بلکه همان نظریه های دانشمندان پیشین خود را به صورت قضایا و برهانهای منطقی عنوان نموده است. در این کتابها بدون هیچ مقدمه ی خاصی به تعریف ساده ی قضیه،سپس به فرضیه های لازم،و بالاخره به‌ بدیهیات‌ یا علوم‌ متعارف‌ می‌پرازد.
به‌ پیروی‌ از دستورات‌ افلاطون‌، خود را مقید به‌ ارقام‌ و شواهدی‌ می‌نمود که‌ جز خط‌کش‌ و پرگار ابزاری‌ نخواهد. اصول مجموعه کتابی است که تنها کتابی‌ که‌ از لحاظ‌ دوام‌ تاریخی‌ با آن‌ برابر است‌ «انجیل‌» است‌.
بسیاری از ریاضیدانان برجسته نخستین گرایش خود را به ریاضیات مدیون کتاب اصول اقلیدس هستند یکی از روشهایی که اقلیدس در این کتاب به کار برده است برهان خلف می باشد برای مثال اگر الف دروغ باشد پس ب راست است . ب دروغ است پس الف راست است .

اثر مفقود اقلیدس‌، ((مقاطع‌ مخروطی‌))، خلاصه‌ی‌ مطالعات‌ منایخموس‌، آریستایوس‌ و دیگران‌ در رشته‌ی‌ مخروطات‌ است‌.

 هندسه ی اقلیدسی:

اقلیدس واضع علم هندسه به شمار می رود. قبل از وی یونانیان و مصریان و بابلیان و اقوام دیگر- از راه تجربه – اطلاعاتی در باب اشکال هندسی و حقایق مربوط به آنها داشتند. ولی این اطلاعات هندسی به صورت مجموعه ای از احکام متفرق بود که هر یک مستقلاً و جدا از سایرین، مورد نظر قرار می گرفت. بدیهی است که این گونه اطلاعات پراکنده و متفرق را نمی توان علم نامید. اقلیدس، با کشف روابط منطقی این احکام و استنتاج بعضی از آنها را از بعضی دیگر اطلاعات پراکنده و جداگانه ی مذکور را تنطیم و تکمیل کرد. از همین جا است که او را پدر و واضع علم هندسه می دانند. «اقلیدس علم هندسه را بر روش قیاسی بنا نهاد. هندسه ی اقلیدسی با چند تعریف و اصل موضوع شروع می شود و سپس استخراج قضایا می آید. تعاریفی که اقلیدس می آورد از این قبیل است:
نقطه آن است که جزء ندارد.
«خط طول بلاعرض است.»«ولی اقلیدس تمام حدود وارد در علم هندسه را تعریف می کند. مثلاً کلماتی را که در دو تعریف مذکور به کار رفته، از قبیل جزء و طول و عرض تعریف نکرده است. اینها از حدود اولیه ی دستگاه اقلیدس است. در تعریفات بعدی از حدودی که قبلاً تعریف شده کمک گرفته می شود. مثلاً وی خط مستقیم را چنین تعریف می کند:
«خط مستقیم خطی است که بین دو انتهای خود هموار باشد.». «اقلیدس در تأسیس علم هندسه احکامی چند را بدون دلیل می پذیرد. وی این احکام را به دو دسته تقسیم می کند که عبارتند از اصل موضوع ها و علوم متعارفی، ولی دلیلی برای این تقسیم اقامه نمی نماید. شاید وی بعضی از احکام مذکور را کلی تر یا واضح تر از بعضی دیگر می پنداشته است. در هر حال هندسه ی اقلیدسی نه فقط مدعی بوده که تمام قضایای آن نتیجه ی منطقی اصل موضوع ها و علوم متعارفی است و مانند آنها راست است، بلکه مدعی بداهت اصل موضوع ها و علوم متعارفی نیز بوده است. این تقسیم بندی در علوم قیاسی امروز منسوخ است. تئوری های قیاسی مدعی آن نیستند که اصل موضوع های آنها فی لبداهه راست است، بلکه هر حکمی از یک تئوری قیاسی که بدون اثبات در آن تئوری پذیرفته شود، اصلی موضوعی از آن تئوری محسوب می شود.
بر اساس هندسه اقلیدس که آن را هندسه مسطحه ودو بعدى مى‏خوانند جهان، نامحدود و بى‏مرز است، این دیدگاه از اصل پنجم برخاسته است که بر اساس آن: دو خط موازى ومستقیم اگر تا بى‏نهایت هم امتداد یابند هیچ‏گاه همدیگر را قطع نمى‏کنند و فاصله‏شان همواره ثابت است. اصل پنجم اقلیدس این است: «اگر خطى بر دو خط راست فرو افتد با آنها دو زاویه بسازد، چنان که مجموعشان از دو قائمه کمتر باشد، وقتى که آن دو خط به طور نامتناهى امتداد داده شوند، در طرفى که زاویه‏هاى کوچکتر از دو قائمه قرار دارند به یکدیگر مى‏رسند».
بسیارى از دانشمندان کوشیدند اصل پنجم اقلیدس را چون چهار اصل دیگر اثبات کنند و موفق نشدند، از جمله مردانى که در اثبات این اصل تلاش کردند:
ابوالحسن ثابت‏بن قره حرانى (221 تا 288ه.ق) پزشک، ریاضى‏دان، اختر شناس و مترجم نامدار بود، وى با روشى که پس از او ابوعلى حسن، مکنى به ابن هیثم،معروف به بصرى (354تا 420ه.ق) پزشک، فیزیکدان، ریاضى‏دان و بزرگترین محقق در شاخه‏ى نورشناسى فیزیک به کار گرفت و همچنین:حکیم ابوالفتح عمر خیام نیشابورى (439 تا 526ه.ق) حکیم، فیلسوف، شاعر، اخترشناس و ریاضى‏دان(همه در اصل پنجم اقلیدس تردید داشتند)، هر کدام خواستند به نحوى آن را اثبات کنند ولى توفیق به دست نیاوردند.
خواجه نصیرالدین حکیم والا مقام خطه‏ى طوس(597 تا 672ه.ق) منجم، ریاضى‏دان، سیاستمدار و نویسنده زبردست نیز در اثبات اصل پنجم به نتیجه‏اى نرسید، وى شرحى به عربى بر اقلیدس و رساله‏اى درباره‏ى اصل‏هاى اقلیدسى نوشت و در بررسى اصل پنجم و براى اثبات آن به اهمیت قضیه‏ى «مجموع زاویه‏هاى مثلث‏برابر دو قائمه است‏» توجه کرده و خواست از این روى کرد نتیجه بگیرد.
جان والیس(1616 تا 1703م) به کار خواجه نصیرالدین و شیوه‏ى استدلال او دلبستگى پیدا کرده و در سال 1651م استدلال او را در کلاس درس دانشگاه اکسفورد به کار برد.
ولی آنگونه که گویند: خود اقلیدس از این اصل و دست آوردهاى آن ناخشنود بود وچشم به پیدایش هندسه نا اقلیدسى دوخت.
کار دیگر و جالبی که توسط خیام انجام شد، نقد و بحثی بود که وی درباره مسائل هندسی که اقلیدس مطرح و اصول هندسی که اقلیدس آنها را تدوین کرده بود، انجام داد. وی به بحث در خصوص تاریخچه بحثهای هندسی در یونان پرداخت و نظرات جدیدی در خوصوص برخی اصول، نظیر اصل مهم هندسه اقلیدسی یعنی اصل توازی مطرح کرد. خیام در این دوره بحثی را آغاز کرد که بعدها باعث گسترش مفهوم عدد شد. در این دوره اعدادی که شناخته شده بودند تنها بخشی از عددهای حقیقی را در بر می گرفتند و هنوز اعداد اصم شناخته شده نبودند. خیام با بحثی که بر سر تعریف نسبت – که در کتاب اصول اقلیدس آمده است بیان می کند تعریف اسلامی نسبت عروف شده جایگزین میکند و سپس با توجه به تعریف جدید مفهومی از نسبت قطر یک مربع به ضلع آن را ارائه می کند. امروزه این عدد را می شناسیم و به عنوان عددی اصم از آن یاد می کنیم؛ اما در زمان خیام این موجودات وجود نداشتند و خیام بر این عقیده بود که باید برای آنها رده جدیدی از اعداد در نظر گرفته شود. تا تعریف نسبت بتواند به طور فراگیر و کامل ادراک شود. این بحثی بود که سرانجام شکافهای موجود در محور اعداد حقیقی را کاهش داد و باعث شد بحث اعداد حقیقی مطرح شود.

هندسه ی نا اقلیدسی:
نیکلای ایوانویچ لباچفسکی،از جمله اولین کسانی بود که قواعد هندسه اقلیدسی را که بیش از 2000 سال بر علوم مختلف ریاضی و فیزیک حاکم بود درهم شکست. کسی باورش نمی شد هنگامی که اروپا مرکز علم بود شخصی در گوشه ای از روسیه بتواند پایه های هندسه اقلیدسی را به لرزه در بیاورد و پایه های علم در قرن نوزدهم را پی ریزی کند.

در میان اصول هندسه اصلی وجود دارد که به این صورت بیان می شود: از هر نقطه خارج یک خط نمی توان بیش از یک خط موازی- در همان صفحه ای که خط و نقطه در آن قرار دارند- به موازات آن خط رسم کرد.
 
در طول سالها این اصل اقلیدس مشکل بزرگی برای ریاضی دانان بود.چرا که ظاهری شبیه به قضیه داشت تا اصل. آنرا با این اصل اقلیدس که می گوید بین هر دو نقطه می توان یک خط راست کشید و یا اینکه همه زوایای قائمه با هم برابر هستند مقایسه کنید.
حقیقت آن است که بسیاری از ریاضی دانان سعی کردند که این اصل اقلیدس را اثبات کنند اما متاسفانه هرگز این امر ممکن نشد. حتی خیام در برخی مقالات خود سعی در اثبات این اصل کرد اما او نیز همانند سایرین به نتیجه نرسید.
لباچفسکی (1792 - 1856) نیز همانند بسیاری از دانشمندان علوم ریاضی سعی در اثبات این اصل کرد و هنگامی که به نتیجه مطلوب نرسید نزد خود به این فکر فرو رفت که این چه هندسه ای است که بر پایه چنین اصل بی اعتباری استوار شده است. اما لباچفسکی در کوشش بعدی خود سعی کرد تا رابطه میان هندسه و دنیای واقعی را پیدا کند.
او معتقد بود اگر نتوانیم از سایر اصول هندسه اقلیدسی این اصل را ثابت کنیم باید به فکر مجموعه اصول دیگری برای هندسه باشیم. اصولی که در دنیای واقعی حضور دارند. او پس از بررسی های بسیار چنین بیان کرد:
“از هر نقطه خارج یک خط می توان لااقل دو خط در همان صفحه به موازات خط رسم کرد ”هر چند پس از این فرض بنظر می رسید که وی در ادامه به تناقض های بسیاری خواهد رسید اما او توانست بر اساس همین فرض و مفروضات قبلی اقلیدس به مجموعه جدید از اصول هندسی برسد که حاوی هیچگونه تناقضی نباشد. او پایه های هندسه ای را بنا نهاد که بعدها کمک بسیار زیادی به فیزیک و مکانیک غیر نیوتنی نمود.
هندسه هذلولوى نا اقلیدسى :

بولیایى (1775تا 1856م) و لباچفسکى(1793 تا 1856م) در اوایل سده نوزدهم هندسه‏ى نااقلیدسى را کشف کردند، اما کشف آن به وسیله‏ى یک کشیش ««زوئیت‏» ایتالیایى تقریبا صد سال پیش تر صورت پذیرفته بود، همچنین اندکى بعد در آلمان:یوهان هاینریخ لامبرت(1718 تا 1777م) نیز به کشف هندسه‏ى نا اقلیدسى بسیار نزدیک شد، به بیان دیگر ،هندسه نا اقلیدسى را نه یک تن بلکه تنى چند در نقاط مختلف جهان بى‏ارتباط به یکدیگر کشف کردند، مثلا گاوس(1777تا 1855م) در آلمان، بولیایى درمجارستان(هنگرى) لباچفسکى در روسیه به این کشف دست‏ یافتند، گاوس همان راه ساکرى و لامبرت که با آثارشان آشنایى داشت را مى‏پیمود، و لباچفسکى نبوغ گاوس را صحه گذاشت و گفت: هیچ برهان قطعى درباره‏ى اصل پنجم وجود ندارد. وى در نظریه‏ى جدید خاطرنشان ساخت که از هر نقطه بیش از یک خطا به موازات خط مفروضى مى‏توان رسم کرد، و مجموع زاویه‏هاى مثلث کمتر از دو قائمه است. کاربرد این هندسه در سطوح منحنى چون سطح یک زین اسب است، و مى‏توان در آن عده‏ى فراوانى خطوط ژئودزى( خطوط مستقیم در سطح مستوى هندسه اقلیدسى) رسم کرد که هیچ یک از آنها هر چه به هر سو هم کشیده شوند یک خط ژئودزى معین را قطع نمى‏کنند.
بر این اساس، در سطح یک زین مجموع سه زاویه مثلثى که تشکیل مى‏شود همواره کوچکتر از دو زاویه قائمه است، و اختلاف بستگى به اندازه مثلث دارد. سطوحى که داراى خواص یک سطح زینى (هندسه هذلولوى) هستند انحناء و سطوح منفى نام دارند.
هندسه نا اقلیدسى بیضوى :برنهاردیمان (1826 تا 1866م) شاگرد گاوس در یک سخنرانى گفت: فضا لازم نیست نامتناهى باشد هر چند بى مرز تصور شود، یعنى مى‏توان گفت: دو خط با هم موازى نیستند و مجموع زاویه‏هاى یک مثلث‏بزرگتر از دو قائمه است و فضا از سه جهت (طول، عرض، ژرفا) بسط یافته است، و این حالت مخالف با سطح زین را با هندسه بر سطح یک کره نشان مى‏دهند، در این حالت کروى خطوط ژئودزى همان قوسهاى دایره عظیمه هستند و هر دو دایره عظیمه غیر مشخص همواره یکدیگر را در دو نقطه قطع مى‏کنند و خطوط موازى به هیچ وجه وجود ندارند.
در این هندسه مجموعه‏ى سه زاویه‏ى مثلث همواره بزرگتر از دو قائمه است .سطوح این هندسه با انحناى مثبت‏شناخته شده‏اند.
روش و طرز کار ریاضى براى توصیف فضاهاى سه بعدى منحنى و نیز فضاهاى منحنى با ابعاد بیشتر توسط ریمان تکمیل شد و براى استفاده اینشتاین وقتى که فکر ملا اتصالى ( زمان و بعد چهارم) را تصور کرد آماده بود.

کیهان شناسى اینشتین :آلبرات اینشتین (1879تا 1955م) کیهان شناسى خود را بر پایه هندسه غیر اقلیدسى بنا نهاد که در آن حجم جهان، محدود تلقى مى‏شود، در هندسه او (بیضوى) سه زاویه مثلث‏بیش از 180 درجه است، و چنان چه خط مستقیمى تا بى‏نهایت ادامه یابد نهایتا به نقطه آغاز برمى‏گردد، یعنى خط مستقیم با انحناء مشخص انحناء مى‏یابد، و این شعاع نشانگر اندازه‏ى جهان است، این نوع جهان فاقد کرانه و فضاى خالى خواهد بود، و کهکشانها و ستارگان با توزیع همگن، کل آن را خواهند پوشاند و تعداد محدودى ستاره و کهکشان در حجم محدود آن وجود خواهند داشت.
طرفداران این نظریه معتقدند با این روش (هندسه بیضوى) امکان دارد به تبیین جهان پرداخت، در این مدل، جهان ایستا و بدون انبساط است، اینشتین به این نکته پى برد که جهان نه همانند مدل «نیوتون‏» نامحدود است و نه مى‏توان محدود و احاطه شده به یک جهان تهى باشد، بلکه فضا با انحناى مثبت‏بیانگر محدودیت جهان است.
در معادلات اینشتین شعاع جهان حدود 20 میلیارد ( 1010×2) پارسک به دست مى‏آید، یعنى تقریبا برابر 20/65 میلیارد سال نورى.
لیکن این نظریه با کشف نسبیت ، با اشکال‏هاى پیچیده و بغرنجى از جانب خود اینشتین روبه رو گشت .
مدل هندسه اقلیدسى از سوى اصل پنجم، دو بعدى بودن و... مخدوش شمرده شده وکوشش‏هاى دانشمندان از خود اقلیدس گرفته تا سایران در استدلالى کردن آن به نتیجه‏اى نرسیده است.

هندسه نااقلیدسى و نسبیت عام اینشتین:در قرن نوزدهم دو ریاضیدان بزرگ به نام «لباچفسکى» و «ریمان» دو نظام هندسى را صورت بندى کردند. که هندسه را از سیطره اقلیدس خارج مى کرد. صورت بندى «اقلیدس» از هندسه تا قرن نوزدهم بسیار پررونق بود و پنداشته مى شد که نظام اقلیدس یگانه نظامى است که امکان پذیر است. این نظام بى چون و چرا توصیفى درست از جهان انگاشته مى شد. هندسه اقلیدسى مدلى براى ساختار نظریه هاى علمى بود و نیوتن و دیگر دانشمندان از آن پیروى مى کردند.
 هندسه اقلیدسى فضایى را مفروض مى گیرد که هیچ گونه خمیدگى و انحنا ندارد. اما نظام هندسى لباچفسکى و ریمانى این خمیدگى را مفروض مى گیرند. (مانند سطح یک کره) همچنین در هندسه هاى نااقلیدسى جمع زوایاى مثلث برابر با ۱۸۰ درجه نیست. (در هندسه اقلیدسى جمع زوایاى مثلث برابر با ۱۸۰ درجه است.) ظهور این هندسه هاى عجیب و غریب براى ریاضیدانان جالب توجه بود اما اهمیت آنها وقتى روشن شد که نسبیت عام اینشتین توسط بیشتر فیزیکدانان به عنوان جایگزینى براى نظریه نیوتن از مکان، زمان و گرانش پذیرفته شد. چون صورت بندى نسبیت عام اینشتین مبتنى بر هندسه((ریمانی)) است. در این نظریه هندسه زمان و مکان به جاى آن که صاف باشد منحنى است. نظریه نسبیت خاص اینشتین تمایز آشکارى میان ریاضیات محض و ریاضیات کاربردى است. هندسه محض مطالعه سیستم هاى ریاضى مختلف است که به وسیله نظام هاى اصول موضوعه متفاوتى توصیف شده اند. اما هندسه محض انتزاعى است و هیچ ربطى با جهان مادى ندارد یعنى فقط به روابط مفاهیم ریاضى با همدیگر، بدون ارجاع به تجربه مى پردازد. هندسه کاربردى، کاربرد ریاضیات در واقعیت است. هندسه کاربردى به وسیله تجربه فراگرفته مى شود و مفاهیم انتزاعى برحسب عناصرى تفسیر مى شوند که بازتاب جهان تجربه اند. نظریه نسبیت، تفسیرى منسجم از مفهوم حرکت، زمان و مکان به ما مى دهد. اینشتین براى تبیین حرکت نور از هندسه نااقلیدسى استفاده کرد. بدین منظور هندسه((ریمانی)) را برگزید.
هندسه اقلیدسى براى دستگاهى مشتمل بر خط هاى راست در یک صفحه طرح ریزى شده است اما در عالم واقع یک چنین خط هاى راستى وجود ندارد. اینشتین معتقد بود امور واقع هندسه ریمانى را اقتضا کرده اند. نور بر اثر میدان هاى گرانشى خمیده شده و به صورت منحنى در مى آید یعنى سیر نورمستقیم نیست بلکه به صورت منحنى ها و دایره هاى عظیمى است که سطح کرات آنها را پدید آورده اند. نور به سبب میدان هاى گرانشى که بر اثر اجرام آسمانى پدید مى آیدخط سیرى منحنى دارد. براساس نسبیت عام نور در راستاى کوتاه ترین خطوط بین نقاط حرکت مى کند اما گاهى این خطوط منحنى هستند چون حضور ماده موجب انحنادر مکان - زمان مى شود.
در نظریه نسبیت عام گرانش یک نیرو نیست بلکه نامى است که ما به اثر انحناى زمان ـ مکان بر حرکت اشیا می دهیم. آزمون هاى عملى ثابت کردند که شالوده عالم نااقلیدسى است و شاید نظریه نسبیت عام بهترین راهنمایى باشد که ما با آن مى توانیم اشیا را مشاهده کنیم. اما مدافعین هندسه اقلیدسى معتقد بودند که به وسیله آزمایش نمى توان تصمیم گرفت که ساختار هندسى جهان اقلیدسى است یا نااقلیدسى. چون مى توان نیروهایى به سیستم مبتنى بر هندسه اقلیدسى اضافه کرد به طورى که شبیه اثرات ساختار نااقلیدسى باشد. نیروهایى که اندازه گیرى هاى ما از طول و زمان را چنان تغییر دهندکه پدیده هایى سازگار با زمان ـ مکان خمیده به وجود آید. این نظریه به((قراردادگرایى)) مشهور است که نخستین بار از طرف ریاضیدان و فیزیکدان فرانسوى((هنرى پوانکاره)) ابراز شد. اما نظریه هایى که بدین طریق به دست مى آوریم ممکن است کاملاً جعلى و موقتى باشند. اما آیا دلایل کافى براى رد آنها وجود دارد؟

اثر امپمبا

شک کردن در مورد اینکه آب گرم زودتر منجمد می‌شود یا آب سرد، ممکن است ساده به نظر برسد

ولی دلایل تقریباً محکم علمی ممکن است شما را به فکر کردن دوباره در این مورد وادار کند.

این اتفاق طبیعی «اثر امپمبا» نام دارد. این نام را به افتخار «اراستو امپمبا» دانش آموز دبیرستانی تانزانیایی که در سال 1963 این اثر را مشاهده و ثبت کرد، انتخاب کرده‌اند.

اثر امپمبا زمانی رخ می‌دهد که دو مقدار مساوی آب با دما‌های متفاوت را در معرض منبع سردی قرار می‌دهند و آبی که دمای بالاتری دارد زودتر منجمد می‌شود.

مشاهده این نوجوان شک‌های دانشمندان و متفکرانی مانند ارستو و دکارت را به یقین تبدیل کرد.

برای توضیح این اثر اولین عاملی که به بحث گذاشته می‌شود، تبخیر سطحی مایع است. مولکول‌های سطحی مایعات همواره در حال جدا شدن از سطح مایع هستند. به همین دلیل است که لیوان آب در دمای معمولی پس از چند روز کاملاً خالی می‌شود و هر قدر که دمای آب بالاتر باشد متعاقباً تبخیر سطحی زودتر رخ می‌دهد.

به این ترتیب در اثر امپمبا، تا زمانی که هر دو مقدار آب منجمد شوند، تبخیر سطحی زودتر در سطح آب با دمای بالاتر انجام می‌شود و با داشتن مقدار کمتری آب برای منجمد شدن، آب با دمای بالاتر زودتر منجمد می‌شود.

ایرادی که به این قسمت وارد است این است که این توضیح برای حالتی درست است که سطح مایع باز باشد و در حالتی که سطح مایع بسته است معنی ندارد و اثر امپمبا در محفظه‌های بسته نیز انجام می‌شود.

توضیح دیگری که برای این اثر می‌دهند، این است که مقدار گاز‌های حل شده در آب گرم کمتر است و به همین دلیل آب گرم زودتر منجمد می‌شود.

دلیل دیگری که ارائه می‌شود این است که در زمان منجمد شدن، آب از پایین به بالا یخ می‌زند و با دارا بودن اختلاف جریان حرکت گرما سریع‌تر انجام می‌شود. به این معنی که هر قدر اختلاف دمای سطح و کف آب در حال انجماد بیشتر باشد، حرکت گرما سریع‌تر انجام می‌شود و به همین دلیل هم آب با دمای بالاتر زودتر منجمد می‌شود.

پس دفعه بعدی که آب را برای یخ زدن در فریزر قرار می‌دهد، سعی کنید از آب گرم استفاده کنید تا زودتر یخ در دسترستان باشد.

امپراطوری روم

امپراتوری روم

از قرن سوم قبل از میلاد، رومیها شروع به تشکیل امپراتوری خود کردند. تا قبل از قرن دوم میلادی، رومی ها بیشتر نواحی غرب اروپا، شرق نزدیک، و شمال آفریقا را تحت کنترل داشتند. موفقیت امپراتوری روم نتیجه استفاده از اژبون های بسیار ورزیده و تعلیم دیده و مدیریت بسیار موثر آنها بود که از مرکز پایتخت رم، به خوبی کنترل می شد.

در سال 27 قبل از میلاد اکتاویان (63 قبل از میلاد ـ 24 میلادی)، اکتاویان یا همان اگوستوس سزار، اولین امپراتور روم می شود. اگوستوس، که به مدت 40 سال بر امپراتوری روم حکومت کرد، مسئولیت اداره آن را با مجلس سنا (گروهی از مسئولین اداره کننده روم)، تقسیم کرد. او از ارتش روم یک نیروی قوی و آموزش دیده ساخت. روم در طول حکومت او دورانی پر از صلح و شکوه را پشت سر نهاد. اگوستوس همچنین در مورد حفظ موقعیت خود بعنوان امپراتور خیلی دقت کرد. او یک گارد محافظ ایجاد کرد که به آنها دستمزد خوبی می داد و آنها را گارد پراتور می نامید.

کالیگولا

اولین امپراتورهای رومی اعضاء خانواده اگوستوس بودند. گایوس سزار (12 ـ 41 میلادی)، که به کالیگولا (به معنی پوتینهای کوچک) معروف بود، در سال 37 میلادی به امپراتوری رسید. سربازان ارتش، که پدرش فرماندهی آنان را به عهده داشت، نام مستعار کالیگولا را به او دادند، چرا که او پوتین های سربازی کوچکی به پا می کرد.

امپراتور دیوانه

بعد از آنکه کالیگولا امپراتور شد، سلامتی عقل خود را از دست داد. یکی از وقایعی که توسط تاریخ نگار رومی سیوتاتیوس 69) ـ 104 میلادی) ثبت شده است، توضیح می دهد که کالیگولا به ارتش بسیار آموزش دیده و قدرتمند خود دستور داد در ساحل دریا صدف حلزون جمع کنند. او به اسب مورد علاقه خود لقب کنسول (عنوان یکی از مسئولین رده بالای روم)، داده بود. وی همچنین با خواهر خود، «دروسیلا» ازوداج کرد، اما بعدا او را کشت. اعضاء گارد محافظ او (پراتورها) در سال 41 میلادی، او را به قتل رسانند.

نرون

آخرین امپراتوری که به خانواده اگوستوس تعلق داشت، نرون (37 ـ 68 میلادی) بود. در سال 54 میلادی، مادر جاه طلب او، آگویپینا 15) ـ 59 میلادی)، شوهر دون خود را مسموم کرد. شوهر امپراتور کلودیوس (10 قبل از میلاد تا 54 میلادی) بود. در نتیجه پسر 17 ساله او جانشین پدر شد. بعد از آغاز امیدوار کننده حکومت او، نرون بی نهایت بی رحم و فاسد شد. وقتی آگویپینا در زندگی خود سرانه فرزندش دخالت کرد، نرون او را کشت. او به خاطر ضیافت های وحشی خود و توهم او در مورد استعدادش در شعر و موسیقی، شهرت داشت.

رم در آتش

در سال 64 میلادی، آتش سوزی بزرگی شهر رم را نابود کرد. نرون تظاهر کرد که قصد داشته تا شهر رم را با طرح جدیدی بازسازی کند. بسیاری از مردم رم عقیده دارند که خود نرون عمدا آتش سوزی را آغاز کرده است. اما به هر حال، نرون گروه مذهبی جدید، یا مسیحیان را مقصر دانست و آنها را کشت. مخالفان حکومت نرون آنقدر قدرت گرفتند که او را مجبور کردند در سال 68 میلادی، خود کشی کند.

سال چهار امپراتور

در سال بعد از مرگ نرون، 4 امپراتور بر سر کار آمدند. یک فرمانده نظامی به نام گالبا (3 قبل از میلاد تا 69 میلادی)، ابتدا قدرت را در دست گرفت. گالبا بوسیله گارد پراتور، کشته شد. این گارد اتو (32 ـ 69 میلادی)، حاکم استان رومی اسپانیا) را به عنوان امپراتور اعلام کرد. لژیون روم که در آلمان مستقر بود، با شنیدن این خبر، فرمانده خود وتیلیوس 15) ـ 69 میلادی)، را به عنوان امپراتور معرفی کردند. وسپاسیان (9 ـ 79 میلادی)، یک فرمانده رقیب، وارد رم شد. او وتیلیوس را کشت و خود امپراتور شد.

انتخابات جانشین

وسپاسیان سنتی را ایجاد کرد که بر اساس آن، یک امپراتور حاکم در طول حکومت خود جانشین خود را انتخاب می کرد. و سپاسیان نظم را به روم بازگرداند. او همچنین یک برنامه ساختمان سازی که شامل استادیوم ورزشی رم بود، آغاز کرد. ساخت این آمفی تئاتر بزرگ که سرگرمیهای عمومی در آن اجرا می شد، در طول حکومت فرزند وسپاسیان، تیتوس 39) ـ 81 میلادی)، که بعد از پدرش به امپراتوری رسید، پایان یافت.

امپراتوری استانی

در قرن دوم میلادی، خانواده های حاکم روم، صاحب نفوذ کمتری در امر انتخاب امپراتور بودند. شهروندان استانهای رومی شروع به اشغال پستهای عالی رتبه در دولت و ارتش، کردند. امپراتورهای بعدی روم از استانهای درون امپراتوری روم، انتخاب می شدند.

تراجان

امپراتور تراجان (53 ـ 117 میلادی) در یکی از استانهای روم به نام آیبیریا «اسپانیای امروز) به دنیا آمد. او یک فرمانده نظامی بزرگ بود و در طول حکومتش، امپراتوری روم از نظر وسعت به اوج خود رسید. وی پیروزیهای نظامی خود را با ساخت بناهای یادبود (ستونهای تراجان)، جشن می گرفت. این ستونها بوسیله مجسمه هایی که پیروزیهای معروف او را نشان می دادند، تزئین شده بودند.

هادریان

پسر خوانده تراجان، هادریان (76 ـ 138 میلادی) بعد از او به امپراتوری روم رسید. هادریان بیشتر دوران حکومتش را به مسافرت در استانهای مختلف امپراتوری روم گذراند. او موانع ثابتی در مقابل حمله بربرها که به این سرزمینها روم حمله می کردند، بنا کرد. نمونه چنین بناهای دفاعی، دیوار هادریان، هنوز در شمال غربی انگلیس باقی مانده اند. هادریان همچنین تغییرات زیادی ایجاد کرد که اداره امپراتوری روم را آسان تر می کرد.

لژیونر رومی

ارتش روم از سربازانی به نام لژیونر تشکیل می شد. یک لژیونر خیلی ورزیده بود. او می توانست در یک روز 32 کیلومتر 20) مایل( در حالیکه یک بسته به وزن 40 کیلو گرم حمل می کرد، راه برود. یونیفورم یک لژیوتر او را در نبردها محافظت می کرد، و در عین حال به او امکان می داد که به آسانی حرکت کند.

800 قبل از میلاد

قوم اتروسک تمدنی را در اقیانوس مرکزی و غربی پدید آورد. اتروسک ها یک مجموعه از مناطق شهری ایجاد کردند.

750 قبل از میلاد

بر اساس افسانه ها، شهر رم بوسیله یک جفت برادر دو قلو، رومولوس و رموس که توسط یک گرگ ماده پرورش یافته بودند، تاسیس شد.

709 قبل از میلاد

تارکوینیوس سوپر باس، که یک پادشاه ستمگر، بود، از رم بیرون رانده شد و حکومت آن کشور تبدیل به جمهوری گردید. (حکومت مردم بر سرنوشت خود(

275 قبل از میلاد

روم تمام ایتالیا را کنترل کرده و توسعه خود را به سمت مدیترانه را آغاز می کند.

264 قبل از میلاد

اولین مرحله از جنگهای کارتاژ آغاز می شود. رومیها وارد جنگ بر علیه کارتاژ، که یک مستعمره فنیقیه ای در شمال آفریقا بود، می شوند.

241 قبل از میلاد

اولین مرحله از جنگهای کارتاژ پایان می پذیرد. جزیره سیسیلی، که قبلا تحت سلطه کارتاژی ها بود، اولین استان رومی می شود.

218 قبل از میلاد

دومین مرحله از جنگهای کارتاژ آغاز می شود. هانیبال، سردار کارتاژی با فیلهای جنگی از کوههای آلپ می گذرد و حمله به ایتالیا را آغاز می کند.

216 قبل از میلاد

هانیبال در جنگ کانای شکست سنگینی به ارتش روم وارد می کند.

202 قبل از میلاد

نیروهای هانیبال در جنگ زاما، در شمال آفریقا، بوسیله ارتش روم به فرماندهی سیپیو افریکانوس شکست می خورد. فیلهای جنگی سپاه کارتاژ، که از صدای شیپورهای جنگی رومیها ترسیده بودند، فرار کردند.

201 قبل از میلاد

دومین مرحله از جنگهای کارتاژ پایان می پذیرد.

149 ـ 146 قبل از میلاد

رومیان طی سومین مرحله از جنگهای کارتاژ سپاهیان کارتاژی را کاملا نابود می کنند.

71 قبل از میلاد

شورش بردگان که توسط گلادیاتوری به نام اسپارتاکوس رهبری می شد. به طور شدیدی در هم کوبیده می شود.

58 قبل از میلاد

ژولیوس سزار فتوحات خود را در سرزمین گل «فرانسه) آغاز می شود.

44 قبل از میلاد

ژولیوس سزار در رم به قتل می رسد. جنگ داخلی آغاز می شود.

31 قبل از میلاد

اکتاویان، پسر خوانده ژولیوس سزار، نیروهای ژنرال رومی مارک آنتونی را شکست می دهد همچنین وی ملکه مصر، کلئوپاترا را در نبرد دریایی اکتیوم ، در مصر شکست میدهد. اکتاویان فرمانروای روم می شود.

27 قبل ار میلاد

مجلس سنای روم عنوان اگوستوس (با شکوه) را به اکتاویان می دهد. اکتاویان به عنوان آگوستوس سزار به عنوان اولین امپراتور روم، انتخاب می شود.

4 قبل از میلاد

عیسی مسیح در یک استان رومی از یهودیه (جنوب فلسطین) به دینا آمد.

43 میلادی

بریتانیا بوسیله رومیان فتح می گردد.

70 میلادی

امپراتور تیتوس انقلاب یهودیان فلسطینی را در هم می کوبد و شهر اورشلیم «بیت المقدس) را تصرف می کند.

212

یک حکم صادره بوسیله کارکالا حق تابعیت (تبعه شدن) را برای همه آزاده ها (مردان آزاد) که در محدوده امپراتوری روم زندگی می کردند، تضمین می نمود.

285

شورش بربرها امپراتوری روم را از شمال تهدید می کرد. امپراطوری بزرگ ایرانیها نیز از شرق امپراتوری روم را تهدید می کردند. امپراتور دیوکلتیانوس کشور را به دو نیم، عامل امپراتوری شرقی و غربی، تقسیم کرد.

313

امپراتور کنستانتین حکم میلان را که آزادی مسیحیت را در سرتاسر قلمرو حکومت تضمین می کرد، صادر کرد.

337

کنستانتین غسل تعمید داده می شود و به دین مسیحیت در می آید.

394
مسیحیت به صورت دین رسمی در می آید.

410

جنگجویان یکی از قبایل بربر به نام، ویزیگوت )گوتهای غربی) به رهبری آلاریک به شهر رم حمله کردند.

452

آتیلای هون به ایتالیا حمله می کند.

476

آخرین امپراتور روم غربی، رومولوس، بوسیله سربازهای بربر که بر ایتالیا غلبه کرده بودند، بیرون رانده شد.

حقایق ثبت شده

قرن واحد ارتش روم بود. هنگامی که در سال 340 قبل از میلاد ارتش روم تشکیل شد. یک قرن شامل 100 سرباز می شد. وقتی فرمانده نظامی رومی، کابوس ماریوس (157 ـ 86 قبل از میلاد) ارتش روم را در سال 100 قبل از میلاد، دوباره سازماندهی کرد، تعداد افراد را در یک قرن به80 نفر کاهش داد. دلیل این کاهش چنین بیان می شد که یک گروه کوچکتر، آسان تر کنترل می شد.

مربع

مربع شکلی هندسی است که از چهار خط (ضلع) برابر تشکیل شده باشد. مربع محیطی بسته دارد و هریک از اضلاعش با دو ضلع دیگر زاویه ۹۰ درجهمی‌سازد. برابر پارسی آن «چهار گوش» یا «چارگوش» است.

برای مربعی با ضلع n داریم:

• محیط: n x ۴
• مساحت: n²

مربع جادویی

'مربع جادویی یا وفقی جدولی است، n * n خانه، که خانه‌های آن با عددهای مثبت از 1 تا n² به ترتیبی پر شده است که مجموع عددهای هر ردیف افقی و یا هر ستون عمودی و یا هر قطر آن، عددی ثابت را نشان دهد. شکل رایج آن شامل اعداد 1 تا n² است ولی گاهی برای کلمات نیز استفاده می‌شود.

این عدد ثابت بدین طریق بدست می‌آید و به آن ثابت جادویی یا جمع جادویی می‌گویند: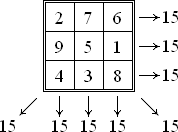

‎

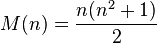
مثلاً ثابت جادویی برای nهای ۳و۴و۵و...برابر است با:

‎

15و34و65و....

چرا اجسام چگال تر از آب پایین تر می روند

آیا تابحال فکر کرده ای که یک کشتی بزرگ چگونه می تواند بدون غرق ‏شدن در روی آب حرکت کند؟ 

آیا می دانی چرا یک کنده درخت در سطح آب به حالت معلق می ماند و ‏هرچه آن را به پایین فشار دهیم و رها کنیم، بلا فاصله به بالای سطح آب ‏می گردد؟ 

چرا اگر یک سنگ در آب بندازیم، بلافاصله در آب فرو می رود و هر چه ‏تلاش کنیم نمی‌توانیم آن را در سطح آب نگاه داریم؟ 

دلیل این پدیده‌های و هزاران پدیده دیگر مانند آنها را که در زندگی ‏د مشاهده می‌کنیم، نیروی ارشمیدس یا نیروی شناور شدن است.‏ 

تعریف شناور شدن: 

هرگاه جسمی را در داخل شاره‌ای غوطه ور کنیم، نیرویی برابر با وزن ‏شاره جابجا می شود. توسط آن ، بر آن وارد می گردد، که این نیرو را ‏نیروی ارشمیدس و یا نیروی شناوری می گویند. این بیان در واقع همان ‏اصل ارشمیدس است که از زمان یونان باستان شناخته شده است.‏ 

آزمایش ساده :‏ 

یک تکه سنگ انتخاب کن. و آن را از یک ترازو آویزان نموده و جرم آن را ‏یادداشت کن. حال آن را در داخل یک ظرف آب فرو ببر و دوباره جرم آن ‏را از روی ترازو بخوان. اختلاف میان دو جرم با جرم آب جابجا شده برابر ‏است. چون چگالی آب برابر هزار کیلو گرم بر متر مربع است، تعداد جرم بر حسب گرم ‏برابر است با حجم بر حسب سانتی متر مکعب ، که با حجم سنگ نیز ‏برابر است. با تقسیم جرم سنگ بر حجم آن چگالی سنگ بدست می ‏آید.‏ 

چرا یک قطعه آهن بر خلاف کنده درخت در آب فرو می رود؟ 

وقتی که یک کنده درخت در آب غوطه ور است، مقداری آب برابر با آب هم ‏حجم خودرا جابجا می کند. اما وزن آب از وزن کنده بیشتر است و لذا ‏نیروی شناوری از نیروی وزن بیشتر است. این قضیه فقط زمانی صادق ‏است که چگالی کنده از چگالی آب کمتر باشد. عموما اگر چگالی شاره از ‏چگالی جسم بیشتر باشد، جسم در شاره شناور می شود. بنابراین ‏دلیل اینکه یک قطعه آهن یا سنگ بلافاصله در داخل آب فرو میرود، این ‏است که چگالی این اجسام از چگالی آب بیشتر است.‏ 

علت غرق شدن یک کشتی بزرگ در دریا :‏ 

اگر در روی جدول‌هایی که در کتاب‌های مختلف وجود دارد، چگالی فولاد را ‏پیدا کنی می بینی که چگالی فولاد هفت برابر چگالی آب ‏است، ولی با وجود این کشتی در آب فرود نمی‌رود. و در سطح آن باقی ‏می ماند. این بدان دلیل است که کشتی عمدتا از هوا تشکیل شده ‏است تا آب. بنابر این ، اگر حجم هوای داخل کشتی را نیز به حساب آوریم، ‏چگالی متوسط کشتی خیلی کمتر از چگالی آب می گردد. بنابراین با ‏ملاحظه هوای داخل کشتی ، چگالی متوسط کشتی از چگالی متوسط ‏آب کمتر خواهد بود.‏

قانون ارشمیدس (شناوری)

هر کس که بخواهد توپی را وارد آب کند حتماً با یک نیروی بازگرداننده قوی مواجه شده است. این نیرو که جهتش رو به بالا است به عنوان "نیروی شناوری" شناخته می‌شود. تمام سیالات به هر جسمی که در آنها قرار می‌گیرد نیرویی وارد می‌کنند.

برای مشاهده فیلم بر روی شکل مقابل تقه بزنید.

منشأ نیروی شناوری از آنجا حاصل می‌شود که فشار با افزایش عمق زیاد می‌گردد.

شکل زیر استوانه‌ای به ارتفاع  را نشان می‌دهد که داخل مایعی قرار گرفته است. فشار  بر روی وجه بالایی نیرویی به اندازه  به سمت پایین وارد می‌کند ( سطح مقطع استوانه است) به همین نحو، فشار روی وجه پایینی، نیرویی به اندازه  رو به بالا وارد می‌کند. از آنجا که فشار در عمق بیشتر زیاد است، نیروی رو به بالا بیشتر از نیروی رو به پایین می‌باشد.

بنابراین، مایع یک نیروی برآیند رو به بالا به استوانه وارد می‌کند اندازه این نیروی شناوری برابر است با:

اگر به جای  مقدر معادلش (یعنی ) را قرار دهیم خواهیم:

حاصل ضرب  برابر حجم مایع داخل استوانه است.  در این رابطه برابر چگالی مایع است نه چگالی ماده‌ای که با آن استوانه ساخته شده است. بنابراین مقدار  برابر جرم  مایع جابجا شده است. پس نیروی شناوری برابر  می‌باشد که این برابر وزن مایع جابجا شده است. این جمله به وزن مایع که بیرون می‌ریزد اشاره دارد مشروط بر اینکه ظرف مایع کاملاً پر باشد و استوانه وارد آن گردد. "نیروی شناوری" نوع جدیدی از نیروهاست. بلکه فقط نامی است که به نیروی برآیند وارده از طرف مایع به جسم اطلاق می‌گردد.

نکته جالب اینکه شکل جسم فرو رفته در آب اهمیت ندارد و مستقل از شکل ظاهری جسم، نیروی شناوری رفتار یگانه دارد و از قانون ارشمیدس پیروی می‌کند. ارشمیدس (٢١٢-٢٨٧ قبل از میلاد) مبانی این قانون را کشف کرد. 
قانون ارشمیدس: 
هر سیالی به جسمی که در آن قرار گرفته (جزئی یا کامل) نیروی شناوری وارد می‌کند. اندازه نیرو برابر وزن سیال جابجا شده است.

	اندازه نیروی شناوری
	وزن مایع جابجا شده

جهت نیروی شناوری نیز همواره در خلاف جهت جاذبه می‌باشد. 
اثری که نیروی شناوری بر جسم می‌گذارد بستگی به سایر نیروهای وارد بر جسم دارد. به عنوان مثال اگر نیروی شناوری به اندازه کافی قوی باشد آنگاه جسم بر روی مایع شناور می‌ماند. شکل‌های زیر این موضوع را نشان می‌دهند.

در شکل مقابل، جسمی به وزن روی مایع قرار دارد و هیچ قسمت از آن را جابجا نمی کند. بنابراین نیروی شناوری به آن وارد نمی گردد.
در شکل مقابل، جسم تا حدودی در مایع فرورفته و در نتیجه نیروی شناوری به آن وارد می‌شود. با این حال، اگر جسم رها گردد آنگاه در مایع فرو می‌رود زیرا نیروی شناوری کوچکتر از وزن جسم است.
در شکل مقابل، جسم آنقدر در مایع فرو رفته که نیروی شناوری وارد بر آن برابر وزن جسم گردیده است. بنابراین جسم به شکل شناور در مایع باقی می‌ماند.

اگر نیروی شناوری قادر به تعادل با نیروی وزن نباشد (حتی در هنگامی که تمام جسم در مایع فرو رفته) آنگاه جسم در مایع غرق می‌شود. حتی وقتی جسم در مایع فرو رفته است با این حال هنوز نیروی شناوری به آن وارد می‌گردد. مثال زیر به ما کمک می‌کند که پیش بینی کنیم آیا جسم در مایع فرو می‌رود یا شناور می‌ماند.

منبع:تبیان

شاخه های علم فیریک

علم فیزیک چند شاخه دارد : گرما - الکترو مغناطیس - مکانیک

خود مکانیک به چند شاخه تقسیم می شود : سینماتیک و ایستا شناسی و ...

اما این نظریات در ادوار گذشته مورد بررسی قرار گرفته و درست در آمده است اما حالا که انسان توانسته به سیارات دیگر برود و این قوانین را در آن جا نیز بررسی کنند و این قوانین غلط از آب در بیایند.

اما شاخه دیگر علم فیزیک الکترومغناطیس را نتوانستند به هم بزنند زیرا قوانین این علم فعلا نیز درست است

و هنوز مثال نادرستی درباره ی این نظریه ها بوجود نیامده است.

علم فیزیک را گرما هم تشکیل داده است اما درباره ی این شاخه مطالب زیادی در دسترس نیست.

حرکت

حرکت یعنی جابه جایی جسمی در اثر وارد شدن نیرو. وقتی که شخصی روی صندلی نشسته باشد و دفتری را ثابت در دست خود گرفته باشد خود فرد آن را ثابت می بیند اما اگر فرد دیگری ساکن باشد و در حال نگاه کردن به این فرد باشد هم خود او و هم دفتر را متحرک می بیند.

این تغییر به این دلیل است که دفتر در روبروی فردی که روی صندلی نشسته است و دارد در یک مسیر با فرد حرکت می کند . اما فردی که ساکن است و در حال نگاه کردن به این پدیده استدفتر را در حال حرکت می بیند.

جابه جایی یعنی خط راستی که مبدا را به مقصد وصل می کند.

مسافت یعنی کل طولی که پیموده ایم.

برای همین اگر فردی از تهران به اصفهان برود و دوباره به تهران برگردد آن وقت جابه جایی نداشته ولی مسافت پیموده است.

رفتار موجی ـ ذره‌ای

در سال 1901 ماکس پلانک (Max Planck: 1947-1858) اولین گام را بسوی مولکول نور برداشت و با استفاده از ایده‌ تقسیم نور ، جواب جانانه‌ای به این سؤال داد. او فرض کرد که انرژی تابشی در هر بسامد v به صورت مضرب صحیحی از hv است، که در آن h یک ثابت طبیعی (معروف به «ثابت پلانک») است. یعنی فرض کرد که انرژی تابشی در بسامد v از «بسته‌های کوچکی با انرژی hv» تشکیل شده است. یعنی اینکه انرژی نورانی ، «گسسته» و «بسته ـ بسته» است.

البته گسسته بودن انرژی به‌تنهایی در فیزیک کلاسیک حرفِ ناجوری نبود، بلکه آنچه گیج‌ کننده بود و آشفتگی را بیشتر می‌کرد، ماهیت «موجی ـ ذره‌ای» نور بود. این تصور که چیزی (مثلاً همین نور) هم بتواند رفتاری مثل رفتار «موج» داشته باشد و هم رفتاری مثل «ذره» ، به طرز تفکر جدیدی در علم محتاج بود.