مسئله
مسئله کوله پشتی چیست؟
فرض کنید که جهانگردی می خواهد کوله پشتی خود را با انتخاب حالتهای ممکن از بین وسائل گوناگونی که بیشترین راحتی را برایش فراهم می سازند پر کند. این مسئله می تواند با شماره گذاری این وسائل از 1 تا n و تعریف برداری از متغیرهای دودویی(Binary) (j 1,2,...n) بصورت ریاضی فرمول بندی شود. به این معنی که: اگر شی ء j ام انتخاب شود در غیر اینصورت وقتی میزان راحتی باشد که وسیله j ا م فراهم می آورد و وزن آن و c اندازه کوله پشتی باشد. مسئله ما انتخاب برداری از بین بردارهای دودویی x است،که محدودیت را بر آورده کند. بطوریکه تابع هدف ماکزیمم مقدار خود را بگیرد به عنوان نمونه ای از مسائلی که می توانند بصورت مساله کوله پشتی فرمول بندی شوند، مسئله زیر را در نظر بگیرید:
فرض کنید که شما مایل به سرمایه گذاری همه یا قسمتی از سرمایه تان باشید. اگر مبلغی که برای سرمایه گذاری در نظر گرفتید c دلار باشد و n مورد برای سرمایه گذاری ممکن باشد ، اجازه دهید که سود حاصل از سرمایه گذاری j ام و مقدار دلار هایی باشد که آن سرمایه گذاری لازم دارد . بدین ترتیب جواب بهینه مسئله کوله پشتی که تعریف کردیم به ما این امکان را می دهد که بهترین حالت ممکن را از بین حالتهای مختلف سرمایه گذاری انتخاب کنیم.
در این رابطه باید روشی برای حل این مسئله پیدا کرد . یک روش ابتدایی که در نگاه اول توجه ما را به خود جلب می کند ، عبارت از برنامه نویسی برای کامپیوتر به منظور امتحان کردن تمامی بردارهای دودویی ممکن x است، تا از بین بردارهایی که محدودیت مسئله را ارضاء می کنند بهترین را انتخاب کند. متاسفانه تعداد چنین بردارهایی است.بطوریکه یک کامپیوتر فرضی که می تواند یک بیلیون بردار را در یک ثانیه امتحان کند؛برای n 60 بیش از 30 سال وقت لازم دارد و بیش از 60 سال برای n 61 و دهها قرن برای n 65 والی اخر.
با این وجود ،با استفاده از الگوریتمهایی خاص می توان در بسیاری موارد مسئله ای با n 100 000 را در عرض چند ثانیه روی یک کامپیوتر کوچک حل کرد.
عدد پی
 |
عدد پی عددگنگی است که در اکثر محاسبات ریاضی به نحوی حضور دارد و از مهمترین اعداد کاربردی در ریاضیات میباشدو آن را با 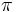 نمایش میدهند. در هندسه اقلیدسی دو بعدی، این عدد را نسبت محیط دایره به قطر دایره و یا مساحت دایره ای به شعاع واحد تعریف میکنند. در ریاضیات مدرن این عدد را در علم آنالیز و با استفاده از توابع مثلثاتی ، به صورت دقیق ریاضی تعریف میکنند.به عنوان نمونه عدد پی رادو برابر کوچکترین مقدار مثبت x ،که به ازای آن cos(x)=0 میشود تعریف میکنند. نمایش میدهند. در هندسه اقلیدسی دو بعدی، این عدد را نسبت محیط دایره به قطر دایره و یا مساحت دایره ای به شعاع واحد تعریف میکنند. در ریاضیات مدرن این عدد را در علم آنالیز و با استفاده از توابع مثلثاتی ، به صورت دقیق ریاضی تعریف میکنند.به عنوان نمونه عدد پی رادو برابر کوچکترین مقدار مثبت x ،که به ازای آن cos(x)=0 میشود تعریف میکنند. |
تاریخچه
بابلیان هنگامی که میخواستند مساحت دایره را حساب کنند،مربع شعاع آن را در 3 ضرب میکردند.البته لوحهای قدیمی تری از بابلیان وجود دارد که مشخص میکند آنها مقدار تقریبی پی را برابر3.125 میدانستند.در مصر باستان مساحت دایره را با استفاده از فرمول محاسبه میکردند.( d قطر دایره در نظر گرفته میشد )که در نتیجه مقدار تقریبی عدد پی 3.1605 بدست میآید.
محاسبه میکردند.( d قطر دایره در نظر گرفته میشد )که در نتیجه مقدار تقریبی عدد پی 3.1605 بدست میآید. 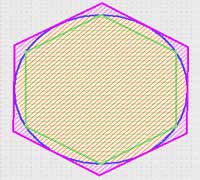 |
تقریب اعشاری عدد پی
اولین نظریه در مورد مقدار تقریبی عدد پی توسط ارشمیدس بیان شد.این نظریه بر پایه تقریب زدن مساحت دایره بوسیله یک شش ضلعی منتظم محیطیو یک شش ضلعی منظم محاطی استوار است. ریاضیدانان اروپایی در قرن هفدهم به مقدار واقعی عدد پی نزدیکتر شدند.از جمله این دانشمندان جیمز گریگوری بود که برای پیدا کردن مقدار عدد پی از فرمول زیر استفاده کرد: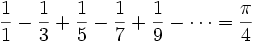
یکی از مشکلاتی که در این روش وجود دارد این است که برای پیدا کردن مقدار عدد پی تا 6 رقم اعشار باید پنج میلیون جمله از سری فوق را با هم جمع کنیم.
در اوایل قرن هجدهم ریاضیدان دیگری به نام جان ماشین فرمول گریگوری را اصلاح کرد که این فرمول امروزه نیز در برنامه های رایانه ای برای محاسبه عدد پی مورد استفاده قرار میگیرد.
این فرمول به صورت زیر است:
 |
با استفاده از این فرمول یک انگلیسی به نام ویلیام شانکس مقدار عدد پی را تا 707 رقم اعشار محاسبه کرد،در حالیکه فقط 527رقم آن درست بود.
امروزه مقدار عدد پی با استفاده از پیشرفته ترین رایانه ها تا میلیونها رقم محاسبه شده است. و تعداد این ارقام هنوز در حال افزایش است.
اعداد اول
عدد اول(انگلیسی: Prime number) عددی طبیعی(Natural number) است که بر هیچ عددی بجز خود و عدد ۱ بخشپذیر نباشد. تنها استثنا عدد ۱ است که جزو این اعداد قرار نمیگیرد. اگرعددی طبیعی وبزرگتر از ۱ اول نباشد مرکب است. علامت اختصاری این اعداد رقم یکان اعداد اول بزرگتر از ۱۰ فقط ممکن است ارقام ۱، ۳، ۷، و ۹ باشد. پیدا کردن ضابطهای جبری برای اعداد اول جزو یکی از معماهای ریاضی باقیمانده است و هنوز کسی به فرمولی برای آنها دست نیافته است. دنبالهٔ اعداد اول به این صورت شروع میشود: ۲، ۳، ۵، ۷، ۱۱، ۱۳، ۱۷، ۱۹، ۲۳، ۲۹، ۳۱، ۳۷، ۴۱، ۴۳، ۴۷، ۵۳، ۵۹، ۶۱، ۶۷، ۷۱، ۷۳، ۷۹، ۸۳، ۸۹، ۹۷، ۱۰۱، ۱۰۳، ۱۰۷، ۱۰۹، ۱۱۳،۱۲۷، ۱۳۱، ۱۳۷، ۱۳۹ (دنبالهی A000040در OEIS به این اثبات دقت کنیداز برهان خلف استفاده می کنیم: فرض خلف : اعداد اول متناهی است. اعداد اول را در هم ضرب می کنیم. P1,P2,P3,...,Pn ضرب اعداد از Pi بزرگتراست. که عدد ۱ جزو اعداد اول نیست پس به تناقض می رسیم و فرض خلف باطل است. اعداد اول نامتناهی هستند. بزرگترین عدد اول کشف شده برابر دو به توان ۳۲ میلیون و ۵۸۲ هزار و ۶۵۷ منهای یک است.این عدد یک عدد مرسن است. عدد مرسن عددی است که برابر ۲ به توان n منهای یک استگ گروه محاسباتی سراوان دیتا که یک گروه محاسباتی ارانی می باشد که در زمینه های مختلف محاسباتی از جمله اعداد اول فعالیت می کند اعداد بسیاری را کشف و محاسبه کرده از جمله تمام اعداد اول یک تا دویست میلیون که از لینک زیر قابل دانلود می باشند تمام اعداد اول یک تا دویست میلیون موسسه Electronic Frontier Foundation جایزه ای به مبلغ صدهزار دلار برای اولین کسی که یک عدد اول با حداقل 10 میلیون رقم پیدا کند در نظر گرفته است.همچنین مبلغ 150 هزار دلار برای کسی که یک عدد اول با 100 میلیون رقم و 250 هزار دلار برای 1 میلیارد رقم در نظر گرفته شده است.این موسسه ممکن است مبلغ 100 هزار دلار برای دپارتمان ریاضی دانشگاه UCLA که موفق به کشف یک عدد اول 13 میلیون رقمی شدند پرداخت کند. یکی از مسائل مورد توجه ریاضیدانان، چگونگی توزیع و ترتیب قرارگرفتن اعداد اول درون رشته اعداد طبیعی است. این چگونگی دارای الگوهایی است که یکی از آنها به «الگوی پیشرفت عددی» معروف است. مسئله مورد توجه اینست که در هر الگوی پیشرفت چند عدد اول پیش از رسیدن به اولین عدد غیر اول، بدست میآیند؟ طولانی ترین رشتهای که تاکنون بدست آمده، ۲۲ عدد اول را شامل است. اولین عدد اول این رشته ۱۱۴۱۰۳۳۷۸۵۰۵۵۳ بوده که اگر عدد ۴۶۰۹۰۹۸۶۹۴۲۰۰ به آن اضافه شود عدد اول بعدی بوجود میآید و میتوان ۲۲ بار عدد مذکور را به اعداد اول مرحله قبل افزود و عدد اولی جدید بدست آورد. دو ریاضیدان اثبات کردهاند برای هر رشته از اعداد اول میتوان به یک رشته عددی رسید.عدد اول
از ویکیپدیا، دانشنامهٔ آزاد
 است.
است.قضیهها






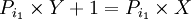
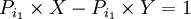
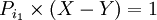
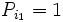
خواص اعداد اول
کشف و محاسبه
جایزه ها برای پیدا کردن اعداد اول
الگوهای توزیع اعداد اول
مثلاً اگر به عدد ۵ که عددی اول است، ۶ واحد اضافه کنیم به ۱۱ و اگر به ۱۱، ۶ واحد اضافه کنیم به ۱۷ و اگر دوباره اضافه کنیم، به ۲۳ و ۲۹ میرسیم که همگی اعدادی اولند. اما با اضافه کردن ۶ واحد دیگر به ۳۵ میرسیم که عددی اول نیست و الگو متوقف میگردد.
هندسه فضایی
مقدمه
هندسه فضایی به بررسی موقعیت اجسام ، اجرام و نقاط متحرک یا ساکن در فضا میپردازد، فضا مختصاتی سه بعدی دارد شامل طول ، عرض ، ارتفاع که این ابعاد را با x ، y و z در صفحه مختصات فضایی نمایش میدهیم. مهمترین مبحث در هندسه فضایی مبحث بردارها میباشند. بنابراین در هندسه فضایی به مؤلفههای برداری ، بردارهای یکه ، صفحات ، فاصلهها و ... خواهیم پرداخت.
مؤلفههای برداری و بردارهای یکه i ، k , j
بعضی از کمیات فیزیکی مانند طول و جرم
اندازه پذیر هستند و توسط اندازهشان کاملا معین میشوند، این کمیات و کمیات نظیر
آنها را کمیات اسکالر میگوئیم. اما کمیات دیگری وجود دارند که علاوه بر اندازه
باید جهت آنها نیز مشخص باشد تا معین شوند این کمیات را کمیات برداری گوئیم. یک
بردار را معمولا با پاره خطی جهتدار نمایش میدهند که جهتش نمایش جهت بردار بوده و
طولش بر حسب یک واحد اختیار شده نمایش اندازهاش میباشد. دو بردار را زمانی مساوی
مینامیم که از لحاظ جهت و اندازه یکسان باشند.
بهترین جبر بردارها مبتنی بر نمایش
آنها بر حسب مؤلفههای موازی محورهای مختصات دکارتی است. این کار با استفاده از واحد طول
یکسان بر سه محور x ، z , y صورت می گیرد و در این راه از بردارهای با طول یک در امتداد
محورها به عنوان بردارهای یکه استفاده میشود که i را بردار یکه محور j ، x را بردار یکه محور y ها و k را بردار یکه محور z ها میگوئیم.
مهمترین ویژگی بردارها در فضا مانند
حالتی است که در صفحه قرار دارند طول و جهت آنها است. طول بردارها با دو بار
استفاده از قضیه فیثاغورس به دست میآید. اما به صورت سادهتر جهت بردار ناصفر
بردار واحدی است که از تقسیم مؤلفههای آن بر طولش به دست میآید.
بردار بین دو نقطه در فضا
بیشتر اوقات لازم است که بردار بین
نقاط ![]() را
بدست آوریم. هندسه فضایی این مشکل را برای ما حل میکند، به این ترتیب که اگر دو
نقطه
را
بدست آوریم. هندسه فضایی این مشکل را برای ما حل میکند، به این ترتیب که اگر دو
نقطه ![]() را
برحسب مختصات فضایی که دارند بیان کنیم بردار بین این دو نقطه توسط رابطه زیر حاصل
خواهد شد:
را
برحسب مختصات فضایی که دارند بیان کنیم بردار بین این دو نقطه توسط رابطه زیر حاصل
خواهد شد:
![]()
فاصله در فضا
برای یافتن فاصله بین دو نقطه ![]() به
مختصات گفته شده در مطلب بالا از مجموع توان دوم هر یک از مؤلفههای فوق رادیکال
با فرجه دوم میگیریم بنابراین داریم:
به
مختصات گفته شده در مطلب بالا از مجموع توان دوم هر یک از مؤلفههای فوق رادیکال
با فرجه دوم میگیریم بنابراین داریم:
![]()
حاصل عبارت فوق یک کمیت اسکالر میباشد.
وسط یک پاره خط در فضا
برای پیدا کردن وسط یک پاره خط که دو
نقطه ![]() را
به هم وصل میکند متوسط و یا به عبارتی میانگین مختصات
را
به هم وصل میکند متوسط و یا به عبارتی میانگین مختصات ![]() را
بدست میآوریم.
را
بدست میآوریم.
کره و استوانه
علاوه بر مطالب فوق هندسه فضایی به
مطالعه کره و استوانه نیز میپردازد. معادله متعارف کره به شعاع a و مرکز ![]() به
صورت زیر است:
به
صورت زیر است:
![]()
در مورد استوانه و مطالعه درباره
استوانه ناچار به تعمیم هندسه تحلیلی به فضا هستیم. به طور کلی استوانه
سطحی است که از حرکت خط مستقیم در امتداد یک منحنی تولید میشود به طوری که همواره
موازی خط میباشد. به طور کلی ، هر منحنی مانند
![]() در
صفحه
در
صفحه ![]() استوانهای
در فضا تعریف میکند که معادله آن به صورت فوق میباشد و از نقاط خطوطی مار بر
منحنی تشکیل شده است که با محور z موازیاند. خطوط را گاهی عناصر استوانه مینامند. بحث فوق را
میتوان برای استوانههایی که عناصرشان موازی سایر محورهای مختصاتاند تکرار کرد.
به طور خلاصه: یک معادله در مختصات دکارتی ، که از آن یکی
از مختصات متغیر حذف شده، نمایش استوانه ای است که عناصرش موازی محور مربوط به
متغیر مفقود است. سهمی گونها یکی دیگر از اشکال مختصات فضایی هستند. بسیاری از
آنتنها به شکل قطعاتی از سهمی گونهای دوارند، رادیو تلسکوپها یکی دیگر از انواع
سهمی گونهای مورد استفاده بشر هستند که در ساخت آنها از هندسه فضایی مدد گرفته شده
است.
استوانهای
در فضا تعریف میکند که معادله آن به صورت فوق میباشد و از نقاط خطوطی مار بر
منحنی تشکیل شده است که با محور z موازیاند. خطوط را گاهی عناصر استوانه مینامند. بحث فوق را
میتوان برای استوانههایی که عناصرشان موازی سایر محورهای مختصاتاند تکرار کرد.
به طور خلاصه: یک معادله در مختصات دکارتی ، که از آن یکی
از مختصات متغیر حذف شده، نمایش استوانه ای است که عناصرش موازی محور مربوط به
متغیر مفقود است. سهمی گونها یکی دیگر از اشکال مختصات فضایی هستند. بسیاری از
آنتنها به شکل قطعاتی از سهمی گونهای دوارند، رادیو تلسکوپها یکی دیگر از انواع
سهمی گونهای مورد استفاده بشر هستند که در ساخت آنها از هندسه فضایی مدد گرفته شده
است.
منشور
منشور قائم شکلی فضایی است که از دو یا چند ضلعی مساوی و موازی تشکیل شده که رئوس این چندضلعیها طوری به هم وصل شده اند که وجوه جانبی این شکل فضایی مستطیل میباشد.
مکعب مستطیل
مکعب مستطیل منشوری است که قاعدههای
آن مستطیل میباشد اگر ابعاد قاعده مکعب مستطیل b , a و ارتفاع آن c باشد خواهیم داشت:
a+b)2c) = مساحت جانبی مکعب مستطیل
(ab+ac+bc)2=2ab+(2bc+2ac)= مساحت کل مکعب مستطیل
Abc= حجم مکعب مستطیل
هرم
هرم شکلی است فضایی که قاعده آن یک یا
چند ضلعی است و وجوه جانبی آن مثلث است. این مثلثها یک رأس مشترک به نام S دارند. هرمی که قاعده آن مربع باشد
هرم مربع القاعده و هرمی که قاعده آن مثلث باشد هرم مثلث القاعده نامیده میشود.
پاره خطی که از رأس هرم بر صفحه قاعده آن عمود میشود ارتفاع نامیده میشود. اگر
قاعده یک هرم یک چند ضلعی منتظم باشد پای ارتفاع آن بر مرکز قاعده منطبق باشد، هرم
را هرم منتظم مینامیم. ارتفاع هر وجه جانبی هرم منتظم را سهم هرم مینامند.
2/سهم×محیط قاعده= مساحت جانبی هرم منتظم
ارتفاع×مساحت قاعده ×3/1 = حجم هرم
مخروط
اگر یک مثلث قائم الزاویه را حول یکی
از اضلاع زاویه قائمه دوران دهیم شکلی فضایی پدید میآید که مخروط نامیده میشود.
در این صورت ضلعی که مثلث را حول آن دوران دادهایم ارتفاع مخروط و ضلع دیگر زاویه
قائمه شعاع قاعده مخروط و وتر مثلث مولد مخروط میباشد.
2 / مولد مخروط×محیط قاعده مخروط = مساحت جانبی مخروط
ارتفاع×مساحت قاعده×3/1 = حجم مخروط
هندسه اقلیدسی
اقلیدس ریاضیدان یونانی،پسر نوقطرس بن برنیقس،ریاضیدان و
منجم بزرگ تاریخ علم،به سال 323 ق.م متولد شد،وی از تبار فنیقی و نخستین
رئیس بخش ریاضیات بود، در زبان یونانی اقلی به معنی کلید و دس به معنای
هندسه و اقلیدس به معنای کلید هندسه است،در آن زمان مرگ اسکندر فرا رسید و
سردارانش برای کسب قدرت با یکدیگر جنگیدند. بطلمیوس یکی از سرداران اسکندر
بود که مصر را گرفت و در آن جا تشکیل حکومت داد. وی از علم و دانش حمایت
می کرد و دانشمندان و دوستداران علم و دانش را دعوت می کرد تا در اسکندریه
اقامت کنند.
اقلیدس بیش از 30 سال نداشت که به خواهش و درخواست
بطلمیوس برای تدریس به اسکندریه رفت و در این شهر مکتب فلسفی خود را پایه
گذاری کرد. اقلیدس مردی محبوب، آرام، فروتن و نیکوکار بود و در حضور
مستبدان و سرداران زورگو در نهایت صراحت صحبت می کرد. بطلمیوس فرمانروای
مصر هنگامی که خواست هندسه را بیاموزد آن را دشوار دید و ترجیح داد که از
راه ساده تری به فهم آن موفق شود، بنابر این از اقلیدس پرسید: آیا امکان
دارد قضایا را به نحو ساده تری بیان کرد؟ اقلیدس به وی جواب داد: غیر ممکن
است، در هندسه راه مخصوص شاهانه وجود ندارد!
وی به مادیات اهمیت چندانی
نمی داد.زمانی که شاگردی از وی پرسید که از هندسه چه نفعی می بریم؟در پاسخ
به وی رو به غلامی کرد و گفت که به شاگردش یک اوبولوس بدهد زیرا که وی می
خواهد از آنچه که می خواند بهره ببرد.وی بسیار متواضع و مهربان بود.
در حدود 300 ق.م ،اقلیدس مدرسه ای را در اسکندریه بنا می کند که به مرکز مطالعات علمی یونان مبدل می گردد.
کتاب
مقدمات اقلیدس یا کتاب هندسه که سه قرن قبل از میلاد به نگارش در آمده، به
زبان های مختلف دنیا ترجمه شده است و از آن زمان که فن چاپ مرسوم شد تا به
حال بیش از2000 بار چاپ گردیده است.زمانیکه این کتاب منتشر شد، چنان
نویسنده اش را مشهور کرد که تا20 قرن بعد هرگونه تغییر در آن به معنی
توهین به مقدسات عالم محسوب می شد. تامدتها مردم بر این تصور بودند که اصل
موضوع های اقلیدس هیچ گاه قابل تغییر نیست و تغییر در آن صورت نمی گیرد،
اما دانشمندان برجسته ای چون ریمان لباچفسکی، علم ریاضیات را توسعه دادند
و هندسه هایی غیراقلیدسی ارائه کردند.اقلیدس نابغه برجسته ای بود که ذوق
سرشاری در زمینه تدوین داشت و این مطلب را می توان با مطالعه کتاب (نور)
به خوبی متوجه شد.
قرن پنجم شاهد اوج قدرت ادبی یونان، قرن
چهارم شاهد شکوفایی فلسفه و قرن سوم شاهد تکامل علوم بود. سلاطین
بیش از دموکراسیها نسبت به تحقیقات علمی گذشت و مساعدت روا
میداشتند. اسکندر کاروانهایی مرکب از جدولهای نجومی بابلی به
شهرهای یونانی سواحل آسیا فرستاد که به زودی به زبان یونانی
ترجمه شدند. بطالسه موزهی مطالعات عالی را بر پا داشتند و علوم و
ادبیات فرهنگهای مدیترانهای را در کتابخانهی کتابخانهی بزرگ خود
متمرکز کردند. بطالسه موزهی مطالعات عالی را بر پا داشتند. آپولونیوس
مقاطع مخروطی خود را به آتالوس اول هدیه کرد،و ارشمیدس تحت حمایت
هیرون دوم به تعیین نسبت محیط دایره به قطر آن و محاسبهی تعداد
ماسههایی که برای پر کردن جهان لازم است پرداخت.
با وجود تمامی
اینها،موفقترین علم نزد آن زمان هندسه بود.اقلیدس متعلق به این دوره می
باشد.حدود 2000 سال است که اقلیدس با علم هندسه یاد می کنیم.ارشمیدس
از دانشمندان باستان نیز دورانی را در نزد شاگردان اقلیدس به تحصیل علم
پرداخت و به ریاضیات اشتیاق فراوانی یافت.
آثار اقلیدس:
اقلیدس مجموعه ای از
13 کتاب را به نام اصول تالیف می کند(کتابهای اول و دوم خلاصهای از
کارهای فیثاغورس در هندسه به دست میدهند، کتاب سوم کارهای بقراط
خیوسی،کتاب پنجم کارهای ائودوکسوس، کتابهای چهارم، ششم و یازدهم و
دوازدهم کارهای فبثاغورسیان متأخر و دانشمندان هندسهی یونانی،
کتابهای هفتم تا دهم از ریاضیات عالی بحث میکنند.)،این کتابها
همچنین زیر بنای ریاضیات جدید را پی می نهند.
که مهمترین کتاب او
می باشد و به عربی ترجمه شده و در سراسر اروپا و خاور میانه گسترش یافت .
کتاب اصول وی در زمینه هندسی یونانی ، جبر و نظریه اعداد نوشته شده است .
که شامل 13 مقاله و 465 قضیه می باشد و در زمینه دایره ، خط راست ، هندسه
فضایی صفحه و کره ، اشکال منتظم ، اعداد گنگ ، استفاده از خط کش و
پرگار در ترسیمات و ..... می باشد که البته اقلیدس مطالب و نظریه های جدید
عنوان نکرده بلکه همان نظریه های دانشمندان پیشین خود را به صورت قضایا و
برهانهای منطقی عنوان نموده است. در این کتابها بدون هیچ مقدمه ی خاصی به
تعریف ساده ی قضیه،سپس به فرضیه های لازم،و بالاخره به بدیهیات یا علوم
متعارف میپرازد.
به پیروی از دستورات افلاطون، خود را مقید به
ارقام و شواهدی مینمود که جز خطکش و پرگار ابزاری نخواهد. اصول
مجموعه کتابی است که تنها کتابی که از لحاظ دوام تاریخی با آن برابر
است «انجیل» است.
بسیاری از ریاضیدانان برجسته نخستین گرایش خود را
به ریاضیات مدیون کتاب اصول اقلیدس هستند یکی از روشهایی که اقلیدس در این
کتاب به کار برده است برهان خلف می باشد برای مثال اگر الف دروغ باشد پس ب
راست است . ب دروغ است پس الف راست است .
اثر مفقود اقلیدس، ((مقاطع مخروطی))، خلاصهی مطالعات منایخموس، آریستایوس و دیگران در رشتهی مخروطات است.
هندسه ی اقلیدسی:
اقلیدس واضع علم هندسه به شمار می رود. قبل از وی
یونانیان و مصریان و بابلیان و اقوام دیگر- از راه تجربه – اطلاعاتی در
باب اشکال هندسی و حقایق مربوط به آنها داشتند. ولی این اطلاعات هندسی به
صورت مجموعه ای از احکام متفرق بود که هر یک مستقلاً و جدا از سایرین،
مورد نظر قرار می گرفت. بدیهی است که این گونه اطلاعات پراکنده و متفرق را
نمی توان علم نامید. اقلیدس، با کشف روابط منطقی این احکام و استنتاج بعضی
از آنها را از بعضی دیگر اطلاعات پراکنده و جداگانه ی مذکور را تنطیم و
تکمیل کرد. از همین جا است که او را پدر و واضع علم هندسه می دانند.
«اقلیدس علم هندسه را بر روش قیاسی بنا نهاد. هندسه ی اقلیدسی با چند
تعریف و اصل موضوع شروع می شود و سپس استخراج قضایا می آید. تعاریفی که
اقلیدس می آورد از این قبیل است:
نقطه آن است که جزء ندارد.
«خط طول بلاعرض است.»«ولی
اقلیدس تمام حدود وارد در علم هندسه را تعریف می کند. مثلاً کلماتی را که
در دو تعریف مذکور به کار رفته، از قبیل جزء و طول و عرض تعریف نکرده است.
اینها از حدود اولیه ی دستگاه اقلیدس است. در تعریفات بعدی از حدودی که
قبلاً تعریف شده کمک گرفته می شود. مثلاً وی خط مستقیم را چنین تعریف می
کند:
«خط مستقیم خطی است که بین دو انتهای خود هموار باشد.». «اقلیدس
در تأسیس علم هندسه احکامی چند را بدون دلیل می پذیرد. وی این احکام را به
دو دسته تقسیم می کند که عبارتند از اصل موضوع ها و علوم متعارفی، ولی
دلیلی برای این تقسیم اقامه نمی نماید. شاید وی بعضی از احکام مذکور را
کلی تر یا واضح تر از بعضی دیگر می پنداشته است. در هر حال هندسه ی
اقلیدسی نه فقط مدعی بوده که تمام قضایای آن نتیجه ی منطقی اصل موضوع ها و
علوم متعارفی است و مانند آنها راست است، بلکه مدعی بداهت اصل موضوع ها و
علوم متعارفی نیز بوده است. این تقسیم بندی در علوم قیاسی امروز منسوخ
است. تئوری های قیاسی مدعی آن نیستند که اصل موضوع های آنها فی لبداهه
راست است، بلکه هر حکمی از یک تئوری قیاسی که بدون اثبات در آن تئوری
پذیرفته شود، اصلی موضوعی از آن تئوری محسوب می شود.
بر اساس هندسه
اقلیدس که آن را هندسه مسطحه ودو بعدى مىخوانند جهان، نامحدود و بىمرز
است، این دیدگاه از اصل پنجم برخاسته است که بر اساس آن: دو خط موازى
ومستقیم اگر تا بىنهایت هم امتداد یابند هیچگاه همدیگر را قطع نمىکنند
و فاصلهشان همواره ثابت است. اصل پنجم اقلیدس این است: «اگر خطى بر دو خط
راست فرو افتد با آنها دو زاویه بسازد، چنان که مجموعشان از دو قائمه کمتر
باشد، وقتى که آن دو خط به طور نامتناهى امتداد داده شوند، در طرفى که
زاویههاى کوچکتر از دو قائمه قرار دارند به یکدیگر مىرسند».
بسیارى
از دانشمندان کوشیدند اصل پنجم اقلیدس را چون چهار اصل دیگر اثبات کنند و
موفق نشدند، از جمله مردانى که در اثبات این اصل تلاش کردند:
ابوالحسن
ثابتبن قره حرانى (221 تا 288ه.ق) پزشک، ریاضىدان، اختر شناس و مترجم
نامدار بود، وى با روشى که پس از او ابوعلى حسن، مکنى به ابن هیثم،معروف
به بصرى (354تا 420ه.ق) پزشک، فیزیکدان، ریاضىدان و بزرگترین محقق در
شاخهى نورشناسى فیزیک به کار گرفت و همچنین:حکیم ابوالفتح عمر خیام
نیشابورى (439 تا 526ه.ق) حکیم، فیلسوف، شاعر، اخترشناس و ریاضىدان(همه
در اصل پنجم اقلیدس تردید داشتند)، هر کدام خواستند به نحوى آن را اثبات
کنند ولى توفیق به دست نیاوردند.
خواجه نصیرالدین حکیم والا مقام
خطهى طوس(597 تا 672ه.ق) منجم، ریاضىدان، سیاستمدار و نویسنده زبردست
نیز در اثبات اصل پنجم به نتیجهاى نرسید، وى شرحى به عربى بر اقلیدس و
رسالهاى دربارهى اصلهاى اقلیدسى نوشت و در بررسى اصل پنجم و براى اثبات
آن به اهمیت قضیهى «مجموع زاویههاى مثلثبرابر دو قائمه است» توجه کرده
و خواست از این روى کرد نتیجه بگیرد.
جان والیس(1616 تا 1703م) به
کار خواجه نصیرالدین و شیوهى استدلال او دلبستگى پیدا کرده و در سال
1651م استدلال او را در کلاس درس دانشگاه اکسفورد به کار برد.
ولی آنگونه که گویند: خود اقلیدس از این اصل و دست آوردهاى آن ناخشنود بود وچشم به پیدایش هندسه نا اقلیدسى دوخت.
کار
دیگر و جالبی که توسط خیام انجام شد، نقد و بحثی بود که وی درباره مسائل
هندسی که اقلیدس مطرح و اصول هندسی که اقلیدس آنها را تدوین کرده بود،
انجام داد. وی به بحث در خصوص تاریخچه بحثهای هندسی در یونان پرداخت و
نظرات جدیدی در خوصوص برخی اصول، نظیر اصل مهم هندسه اقلیدسی یعنی اصل
توازی مطرح کرد. خیام در این دوره بحثی را آغاز کرد که بعدها باعث گسترش
مفهوم عدد شد. در این دوره اعدادی که شناخته شده بودند تنها بخشی از
عددهای حقیقی را در بر می گرفتند و هنوز اعداد اصم شناخته شده نبودند.
خیام با بحثی که بر سر تعریف نسبت – که در کتاب اصول اقلیدس آمده است بیان
می کند تعریف اسلامی نسبت عروف شده جایگزین میکند و سپس با توجه به تعریف
جدید مفهومی از نسبت قطر یک مربع به ضلع آن را ارائه می کند. امروزه این
عدد را می شناسیم و به عنوان عددی اصم از آن یاد می کنیم؛ اما در زمان
خیام این موجودات وجود نداشتند و خیام بر این عقیده بود که باید برای آنها
رده جدیدی از اعداد در نظر گرفته شود. تا تعریف نسبت بتواند به طور فراگیر
و کامل ادراک شود. این بحثی بود که سرانجام شکافهای موجود در محور اعداد
حقیقی را کاهش داد و باعث شد بحث اعداد حقیقی مطرح شود.
هندسه ی نا اقلیدسی:
نیکلای
ایوانویچ لباچفسکی،از جمله اولین کسانی بود که قواعد هندسه اقلیدسی را که
بیش از 2000 سال بر علوم مختلف ریاضی و فیزیک حاکم بود درهم شکست. کسی
باورش نمی شد هنگامی که اروپا مرکز علم بود شخصی در گوشه ای از روسیه
بتواند پایه های هندسه اقلیدسی را به لرزه در بیاورد و پایه های علم در
قرن نوزدهم را پی ریزی کند.
در میان اصول هندسه اصلی وجود دارد که به این صورت
بیان می شود: از هر نقطه خارج یک خط نمی توان بیش از یک خط موازی- در همان
صفحه ای که خط و نقطه در آن قرار دارند- به موازات آن خط رسم کرد.
در
طول سالها این اصل اقلیدس مشکل بزرگی برای ریاضی دانان بود.چرا که ظاهری
شبیه به قضیه داشت تا اصل. آنرا با این اصل اقلیدس که می گوید بین هر دو
نقطه می توان یک خط راست کشید و یا اینکه همه زوایای قائمه با هم برابر
هستند مقایسه کنید.
حقیقت آن است که بسیاری از ریاضی دانان سعی کردند
که این اصل اقلیدس را اثبات کنند اما متاسفانه هرگز این امر ممکن نشد. حتی
خیام در برخی مقالات خود سعی در اثبات این اصل کرد اما او نیز همانند
سایرین به نتیجه نرسید.
لباچفسکی (1792 - 1856) نیز همانند بسیاری از
دانشمندان علوم ریاضی سعی در اثبات این اصل کرد و هنگامی که به نتیجه
مطلوب نرسید نزد خود به این فکر فرو رفت که این چه هندسه ای است که بر
پایه چنین اصل بی اعتباری استوار شده است. اما لباچفسکی در کوشش بعدی خود
سعی کرد تا رابطه میان هندسه و دنیای واقعی را پیدا کند.
او معتقد بود
اگر نتوانیم از سایر اصول هندسه اقلیدسی این اصل را ثابت کنیم باید به فکر
مجموعه اصول دیگری برای هندسه باشیم. اصولی که در دنیای واقعی حضور دارند.
او پس از بررسی های بسیار چنین بیان کرد:
“از هر نقطه خارج یک خط می توان لااقل دو خط در همان صفحه به موازات خط رسم کرد ”هر
چند پس از این فرض بنظر می رسید که وی در ادامه به تناقض های بسیاری خواهد
رسید اما او توانست بر اساس همین فرض و مفروضات قبلی اقلیدس به مجموعه
جدید از اصول هندسی برسد که حاوی هیچگونه تناقضی نباشد. او پایه های هندسه
ای را بنا نهاد که بعدها کمک بسیار زیادی به فیزیک و مکانیک غیر نیوتنی
نمود.
هندسه هذلولوى نا اقلیدسى :
بولیایى (1775تا 1856م) و لباچفسکى(1793 تا 1856م) در
اوایل سده نوزدهم هندسهى نااقلیدسى را کشف کردند، اما کشف آن به وسیلهى
یک کشیش ««زوئیت» ایتالیایى تقریبا صد سال پیش تر صورت پذیرفته بود،
همچنین اندکى بعد در آلمان:یوهان هاینریخ لامبرت(1718 تا 1777م) نیز به
کشف هندسهى نا اقلیدسى بسیار نزدیک شد، به بیان دیگر ،هندسه نا اقلیدسى
را نه یک تن بلکه تنى چند در نقاط مختلف جهان بىارتباط به یکدیگر کشف
کردند، مثلا گاوس(1777تا 1855م) در آلمان، بولیایى درمجارستان(هنگرى)
لباچفسکى در روسیه به این کشف دست یافتند، گاوس همان راه ساکرى و لامبرت
که با آثارشان آشنایى داشت را مىپیمود، و لباچفسکى نبوغ گاوس را صحه
گذاشت و گفت: هیچ برهان قطعى دربارهى اصل پنجم وجود ندارد. وى در نظریهى
جدید خاطرنشان ساخت که از هر نقطه بیش از یک خطا به موازات خط مفروضى
مىتوان رسم کرد، و مجموع زاویههاى مثلث کمتر از دو قائمه است. کاربرد
این هندسه در سطوح منحنى چون سطح یک زین اسب است، و مىتوان در آن عدهى
فراوانى خطوط ژئودزى( خطوط مستقیم در سطح مستوى هندسه اقلیدسى) رسم کرد که
هیچ یک از آنها هر چه به هر سو هم کشیده شوند یک خط ژئودزى معین را قطع
نمىکنند.
بر این اساس، در سطح یک زین مجموع سه زاویه مثلثى که تشکیل
مىشود همواره کوچکتر از دو زاویه قائمه است، و اختلاف بستگى به اندازه
مثلث دارد. سطوحى که داراى خواص یک سطح زینى (هندسه هذلولوى) هستند انحناء
و سطوح منفى نام دارند.
هندسه نا اقلیدسى بیضوى :برنهاردیمان
(1826 تا 1866م) شاگرد گاوس در یک سخنرانى گفت: فضا لازم نیست نامتناهى
باشد هر چند بى مرز تصور شود، یعنى مىتوان گفت: دو خط با هم موازى نیستند
و مجموع زاویههاى یک مثلثبزرگتر از دو قائمه است و فضا از سه جهت (طول،
عرض، ژرفا) بسط یافته است، و این حالت مخالف با سطح زین را با هندسه بر
سطح یک کره نشان مىدهند، در این حالت کروى خطوط ژئودزى همان قوسهاى دایره
عظیمه هستند و هر دو دایره عظیمه غیر مشخص همواره یکدیگر را در دو نقطه
قطع مىکنند و خطوط موازى به هیچ وجه وجود ندارند.
در این هندسه مجموعهى سه زاویهى مثلث همواره بزرگتر از دو قائمه است .سطوح این هندسه با انحناى مثبتشناخته شدهاند.
روش
و طرز کار ریاضى براى توصیف فضاهاى سه بعدى منحنى و نیز فضاهاى منحنى با
ابعاد بیشتر توسط ریمان تکمیل شد و براى استفاده اینشتاین وقتى که فکر ملا
اتصالى ( زمان و بعد چهارم) را تصور کرد آماده بود.
کیهان شناسى اینشتین :آلبرات
اینشتین (1879تا 1955م) کیهان شناسى خود را بر پایه هندسه غیر اقلیدسى بنا
نهاد که در آن حجم جهان، محدود تلقى مىشود، در هندسه او (بیضوى) سه زاویه
مثلثبیش از 180 درجه است، و چنان چه خط مستقیمى تا بىنهایت ادامه یابد
نهایتا به نقطه آغاز برمىگردد، یعنى خط مستقیم با انحناء مشخص انحناء
مىیابد، و این شعاع نشانگر اندازهى جهان است، این نوع جهان فاقد کرانه و
فضاى خالى خواهد بود، و کهکشانها و ستارگان با توزیع همگن، کل آن را
خواهند پوشاند و تعداد محدودى ستاره و کهکشان در حجم محدود آن وجود خواهند
داشت.
طرفداران این نظریه معتقدند با این روش (هندسه بیضوى) امکان
دارد به تبیین جهان پرداخت، در این مدل، جهان ایستا و بدون انبساط است،
اینشتین به این نکته پى برد که جهان نه همانند مدل «نیوتون» نامحدود است
و نه مىتوان محدود و احاطه شده به یک جهان تهى باشد، بلکه فضا با انحناى
مثبتبیانگر محدودیت جهان است.
در معادلات اینشتین شعاع جهان حدود 20 میلیارد ( 1010×2) پارسک به دست مىآید، یعنى تقریبا برابر 20/65 میلیارد سال نورى.
لیکن این نظریه با کشف نسبیت ، با اشکالهاى پیچیده و بغرنجى از جانب خود اینشتین روبه رو گشت .
مدل
هندسه اقلیدسى از سوى اصل پنجم، دو بعدى بودن و... مخدوش شمرده شده
وکوششهاى دانشمندان از خود اقلیدس گرفته تا سایران در استدلالى کردن آن
به نتیجهاى نرسیده است.
هندسه اقلیدسى فضایى را مفروض مى گیرد که هیچ گونه خمیدگى و انحنا ندارد. اما نظام هندسى لباچفسکى و ریمانى این خمیدگى را مفروض مى گیرند. (مانند سطح یک کره) همچنین در هندسه هاى نااقلیدسى جمع زوایاى مثلث برابر با ۱۸۰ درجه نیست. (در هندسه اقلیدسى جمع زوایاى مثلث برابر با ۱۸۰ درجه است.) ظهور این هندسه هاى عجیب و غریب براى ریاضیدانان جالب توجه بود اما اهمیت آنها وقتى روشن شد که نسبیت عام اینشتین توسط بیشتر فیزیکدانان به عنوان جایگزینى براى نظریه نیوتن از مکان، زمان و گرانش پذیرفته شد. چون صورت بندى نسبیت عام اینشتین مبتنى بر هندسه((ریمانی)) است. در این نظریه هندسه زمان و مکان به جاى آن که صاف باشد منحنى است. نظریه نسبیت خاص اینشتین تمایز آشکارى میان ریاضیات محض و ریاضیات کاربردى است. هندسه محض مطالعه سیستم هاى ریاضى مختلف است که به وسیله نظام هاى اصول موضوعه متفاوتى توصیف شده اند. اما هندسه محض انتزاعى است و هیچ ربطى با جهان مادى ندارد یعنى فقط به روابط مفاهیم ریاضى با همدیگر، بدون ارجاع به تجربه مى پردازد. هندسه کاربردى، کاربرد ریاضیات در واقعیت است. هندسه کاربردى به وسیله تجربه فراگرفته مى شود و مفاهیم انتزاعى برحسب عناصرى تفسیر مى شوند که بازتاب جهان تجربه اند. نظریه نسبیت، تفسیرى منسجم از مفهوم حرکت، زمان و مکان به ما مى دهد. اینشتین براى تبیین حرکت نور از هندسه نااقلیدسى استفاده کرد. بدین منظور هندسه((ریمانی)) را برگزید.
هندسه اقلیدسى براى دستگاهى مشتمل بر خط هاى راست در یک صفحه طرح ریزى شده است اما در عالم واقع یک چنین خط هاى راستى وجود ندارد. اینشتین معتقد بود امور واقع هندسه ریمانى را اقتضا کرده اند. نور بر اثر میدان هاى گرانشى خمیده شده و به صورت منحنى در مى آید یعنى سیر نورمستقیم نیست بلکه به صورت منحنى ها و دایره هاى عظیمى است که سطح کرات آنها را پدید آورده اند. نور به سبب میدان هاى گرانشى که بر اثر اجرام آسمانى پدید مى آیدخط سیرى منحنى دارد. براساس نسبیت عام نور در راستاى کوتاه ترین خطوط بین نقاط حرکت مى کند اما گاهى این خطوط منحنى هستند چون حضور ماده موجب انحنادر مکان - زمان مى شود.
در نظریه نسبیت عام گرانش یک نیرو نیست بلکه نامى است که ما به اثر انحناى زمان ـ مکان بر حرکت اشیا می دهیم. آزمون هاى عملى ثابت کردند که شالوده عالم نااقلیدسى است و شاید نظریه نسبیت عام بهترین راهنمایى باشد که ما با آن مى توانیم اشیا را مشاهده کنیم. اما مدافعین هندسه اقلیدسى معتقد بودند که به وسیله آزمایش نمى توان تصمیم گرفت که ساختار هندسى جهان اقلیدسى است یا نااقلیدسى. چون مى توان نیروهایى به سیستم مبتنى بر هندسه اقلیدسى اضافه کرد به طورى که شبیه اثرات ساختار نااقلیدسى باشد. نیروهایى که اندازه گیرى هاى ما از طول و زمان را چنان تغییر دهندکه پدیده هایى سازگار با زمان ـ مکان خمیده به وجود آید. این نظریه به((قراردادگرایى)) مشهور است که نخستین بار از طرف ریاضیدان و فیزیکدان فرانسوى((هنرى پوانکاره)) ابراز شد. اما نظریه هایى که بدین طریق به دست مى آوریم ممکن است کاملاً جعلى و موقتى باشند. اما آیا دلایل کافى براى رد آنها وجود دارد؟
مربع
مربع شکلی هندسی است که از چهار خط (ضلع) برابر تشکیل شده باشد. مربع محیطی بسته دارد و هریک از اضلاعش با دو ضلع دیگر زاویه ۹۰ درجهمیسازد. برابر پارسی آن «چهار گوش» یا «چارگوش» است.
برای مربعی با ضلع n داریم:
- محیط: n x ۴
- مساحت: n2
مربع جادویی
'مربع جادویی یا وفقی جدولی است، n * n خانه، که خانههای آن با عددهای مثبت از 1 تا n² به ترتیبی پر شده است که مجموع عددهای هر ردیف افقی و یا هر ستون عمودی و یا هر قطر آن، عددی ثابت را نشان دهد. شکل رایج آن شامل اعداد 1 تا n² است ولی گاهی برای کلمات نیز استفاده میشود. این عدد ثابت بدین طریق بدست میآید و به آن ثابت جادویی یا جمع جادویی میگویند: 15و34و65و....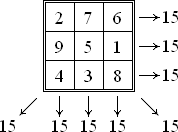
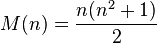
مثلاً ثابت جادویی برای nهای ۳و۴و۵و...برابر است با:
چرا باید ریاضی بخوانیم
چرا باید ریاضیات بخوانیم؟ (ولادیمر ارنولد)
چرا باید ریاضیات بخوانیم؟راجر بیکن فیلسوف انگلیسی در سال 1267 میلادی پاسخ این سوال را چنین داده است:
(کسی این کار را نکند نمیتواند چیزی از بقیه علوم و هر آنچه دراین جهان است بفهمد...چیزی که بدتر است این است که کسانی که ریاضیات نمیدانند به جهالت خودشان پی نمی برند ودر نتیجه در پی چاره جویی بر نمی آیند.))
می توانم همین جا سخنرانیم را پایان دهم اما ممکن است بعضیها فکر کنند که شاید خیلی چیزها در هفت قرن گذشته تغییر کرده باشد....
شاهدی تازه تر می آورم پال دیراک از خالقان مکانیک کوانتومی معتقد است که وقتی تئوری فیزیکی ای را پایه ریزی می کنید نبایدبه هیچ شهود فیزیکی ای اعتماد کنید.پس به چه چیزی اعتماد کنید؟به گفته ی این فیزیکدان مشهور فقط به برنامه ای متکی بر ریاضیات _ولو اینکه در نگاه اول ربطی به فیزیک نداشته باشد.
در حقیقت در فیزیک تمامی ایده های صرفا فیزیکی رایج در ابتدای این قرن را کنار گذاشته اند در حالی که الگوهای ریاضی ای که به زرادخانه فیزیکدان ها راه یافته اند به تدریج معنای فیزیکی یافته اند.در اینجاستکه قابل اعتماد بودن ریاضیات به روشنی رخ مینمایاند.
بنابراین الگوسازی ریاضی روشی پربار برای شناخت در علوم طبیعی است.اکنون می خواهیم الگوهای ریاضی را از نگاهی دیگر یعنی مسئله ی آموزش ریاضی بررسی کنیم.
سه روش اموزش ریاضیات
در اموزش ریاضیات روسی (هم در دبیرستان و هم در مقاطع بالاتر) ما پیرو نظام اموزشی اروپایی هستیم که بر اساس ((بورباکی ای سازی))ریاضیات بنا شده است (نیکلاس بورباکی نام مستعار گروهی از ریاضیدانان فرانسوی است که ازسال 1939 به انتشار مجموعه ای از کتابها دست زده اندکه در انها شاخه های اصلی ریاضیات جدید به طور اصولی_یعنی به روش اصل موضوعی براساس نظریه ی مجموعه ها_شرح داده شده است.)
اصولی کردن ریاضیات به نوعی تصنعی کردن آموزش آن منجر می شود واین زیانی است که بورباکی ای سازی به آموزش ریاضیات وارد کرده است.نمونه ای شگرف مثال زیر است:
از دانش آموز سال_دومی مدرسه ای در فرانسه پرسیده اند ((دو بعلاوه ی سه چقدر میشود؟)) پاسخ چنین بود ((چون جمع تعویض پذیر است می شود سه بعلاوه ی دو.))
پاسخی واقعا قابل تامل! کاملا درست است اما دانش آموزان حتی به جمع کردن ساده ی این دو عدد هم فکر نکرده اند زیرا در تعلیم انها تکیه بر ویژگی های عملها بوده است. در اروپا معلمان متوجه نارساییهای این روش شده اند و بورباکی ای سازی را کنار گذاشته اند.
طی چند سال گذشته آموزش ریاضیات روسی دستخوش تغییراتی به سبک آمریکایی شده است.اساس این سبک این اصل است: آنچه را که برای کاربردهای عملی لازم است آموزش بدهید.در نتیجه کسی که فکر می کند به ریاضیات احتیاجی نخواهد داشت اصلآ لازم نیست ان را بخواند.ریاضیات درسی اختیاری در دوره ی راهنمایی و دبیرستان است_مثلآ یک سوم دانش آموزان دبیرستانی جبر نمی خوانند.نتیجه ی این امر را در مثال زیر روشن کرده ایم:
در آزمونی برای دانش آموزان چهارده ساله ی آمریکایی از آنها خواسته شده بود که برآورد کنند (نه اینکه حساب کنند بلکه برآورد کنند) که اگر 80 درصد از عدد 120 رابرداریم این عدد چه تغییری می کند.سه نوع پاسخ را می توانستند انتخاب کنند: زیاد میشود،تغییری نمیکند،کمتر میشود.تقریبآ 30 درصد دانش آموزان سوال شونده پاسخ درست را برگزیده بودند.یعنی اینکه پاسخها را تصادفی انتخاب کرده بودند.نتیجه: هیچ کس هیچ چیز نمی داند.دومین ویژگی شاخص روش آموزش ریاضی آمریکایی،کامپیوتری کردن آن است.
جذابییت کار با کامپیوتر به خودی خود به گسترش تواناییهای فکری کمکی نمی کند.مثالی دیگر از یکی از آزمونهای آمریکا میاوریم:
کلاسی 26 دانش آموز دارد.این دانش آموزان می خواهند با اتومبیل به مسافرت بروند.در هر اتومبیل یک نفر از اولیا و چهار دانش آموزجا می شوند.چند نفر از اولیا را میتوانیم دعوت کنیم؟
جوابی که همه داده بودند 65 نفر بود جواب کامپیوتر :
است،ودانش آموزان می دانستند که اگر جواب باید عددی صحیح باشد،می توان بلایی سر ممیز آورد_مثلآ می توان اصلآ آن را برداشت.
نمونه ی دیگری از یکی از آزمونهای رسمی دانش آموزی در سال 1992 می آوریم:
رابطه ی کدام زوج شباهت بیشتری به رابطه ی میان زاویه و درجه دارد:
الف) زمان وساعت
ب) شیر وکوارت ((واحد اندازه گیری مایعات برابر با 44/1 لیتر))
ج) مساحت و اینچ مربع
پاسخ،مساحت و اینچ مربع است،زیرا درجه ی کوچکترین واحد اندازه گیری زاویه و اینچ مربع کوچکترین واحد اندازه گیری مساحت است،اما ساعت را می توان به دقیقه هم تقسیم کرد.
طراح این مسئله مسلمآ مطابق نظام امریکایی می اندیشیده است.می ترسم که طولی نکشد که ما هم به چنین سطح نازلی برسیم.( جو برمن،استاد ریاضی در نیویورک توضیح داده که( از نظر او که آمریکایی است) ،پاسخ درست این مسئله کاملآ روشن است.او گفت که ((اصل مطلب این است که من می توانم میزان حماقت طراح این مسئله را دقیقآ تصور کنم.))_) مایه ی شگفتی است که تعداد زیادی ریاضیدان و فیزیکدان برجسته در ایالات متحده وجود دارد.
امروزه آموزش ریاضیات ما آرام آرام از نظام اروپایی به نظام آمریکایی تبدیل می شود.مطابق معمول ،باز هم عقبیم،حدود سی سال از اروپا عقبتریم و بنابراین سی سال بعد زمان آن فرا میرسد که اوضاع را سروسامان بدهیم و از چاهی که با ظناب نظام آموزشی آمریکایی به آن رفته ایم بیرون بیاییم.
سطح آموزش ریاضی سنتی ما بسیار بالا و بر اساس آموزش مسئله های حساب بوده است.حتی تا همین بیست سال پیش هم خانواده هایی بودند که نسخه هایی از کتابهای قدیمی مربوط به مسئله های ((سود و زیان)) را داشتند.در حال حاضر، همه ی اینها از بین رفته است.در آخرین اصلاحات آموزش ریاضی،جبری سازی، دانش آموزان را به روبات تبدیل کرده است.
مساله های حساب است که ((بی محتوایی)) ریاضیاتی را که تدریس می کنیم نشان می دهند مثلآ این مسئله را در نظر بگیرید:
1.سه تا سیب داریم.یکی را برمی داریم.چند تا باقی مانده است؟
2.چند برش با اره لازم است تا تکه ای هیزم را به سه بخش تقسیم کنیم؟
3.تعداد خواهران بوریس از تعداد برادرانش بیشتر است.در خانواده ی او تعداد دختران چند تا بیشتر از تعداد پسران است؟
از منظر حساب اینها مساله های متفاوتی هستند،زیرا محتوایشان فرق می کند.همچنین،تلاش فکری لازم برای حل کردن مسئله ها هم کاملآ متفاوت است،هر چند که الگوی جبری هر یک از آنها یکی است: 2=1-3 جالب توجه ترین نکته در ریاضیات،فراگیر بودن شگفت آور الگوها و کارایی نامحدود انها در مساله های علمی است.
به قول ولادیمیر مایاکوفسکی،شاعر بزرگ روس: ((کسی که اولین بار دو بعلاوه ی دو می شود چهار را، مطرح کرده است حتی اگر با جمع کردن دو تا ته سیگار با دو تا ته سیگار دیگر به این حقیقت رسیده باشد،ریاضیدان بزرگی بوده است.هر کس پس از او به این نتیجه رسیده باشد،حتی اگر چیزهای بسیار بزرگتری،مثل لوکوموتیوها را با هم جمع کرده باشد،ریاضیدان نیست)) لوکوموتیو شماری،روش آمریکایی آموزش ریاضیات است.چنین چیزی مصیبت بار است.طرز پیشرفت فیزیک در ابتدای سال اخیر نمونه ای است که نشان می دهد ریاضیات لوکوموتیوی به مراتب از ریاضیات ته سیگاری به درد نخورتر است:ریاضیات کاربردی نتوانسته همگام با فیزیک پیشترفت کند،در حالی که ریاضیات نظری هر آنچه را که فیزیکدانان برای بسط بیشتر دانش خودشان نیاز داشته اند برایشان فراهم کرده است.ریاضیات لوکوموتیوی از روال معمول عقب می ماند: تا حساب کردن با چرتکه را آموزش بدهیم،سر و کله ی کامپیوترها پیدا می شود .باید شیوه ی فکر کردن را آموزش بدهیم،نه طرز فشار دادن دکمه ها را.
استقرا
منبع : سایت رشد استقرا
مقدمه
برای درک مفهوم استقرا به مراحل اثبات یکی از برابریهای ساده در ریاضیات توجه کنید:
مجموع اعداد طبیعی زیر را در نظر بگیرید: 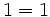

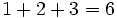
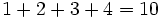

اگر به طور که بخواهیم 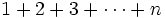 را بدست بیاوریم یک راه این است که الگویی از مجموع اعداد بالا بدست آورده و سعی در اثبات آن نمائیم.
را بدست بیاوریم یک راه این است که الگویی از مجموع اعداد بالا بدست آورده و سعی در اثبات آن نمائیم. 
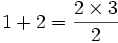
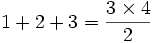

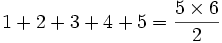
و به این ترتیب الگوی 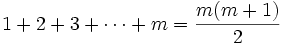 را برای مجموعة فوق در نظر میگیریم.
را برای مجموعة فوق در نظر میگیریم.
این الگو در حقیقت یک گزاره بر روی اعداد طبیعی میباشد که میتوان آن را با  به معنی
به معنی  نمایش داد.
نمایش داد.
اگر چه اثبات این الگو به طور مستقیم و بدون کمک به استقرا به سادگی ممکن میباشد ولی در حل مسائل ریاضی به دفعات به حدسهایی برمیخوریم که اثبات آنها میتواند مشکل باشد در ایدة استقرا یکی از زیباترین ایدههای موجود برای کمک به ما میباشد.
برای آنکه بیشتر آمادگی ذهنی برای درک استقرا پیدا کنیم به همان مثال مجموع اعداد 1 تا  میرویم، و میخواهیم گزارة
میرویم، و میخواهیم گزارة  را که گزارهای دربارة عدد
را که گزارهای دربارة عدد  میباشد ثابت کنیم.
میباشد ثابت کنیم.
در ایدة استقرا که جلوتر به تعریف دقیق آن میپردازیم نخست باید برای  های کوچک درستی
های کوچک درستی  را نشان دهیم مانند:
را نشان دهیم مانند: 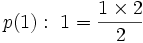
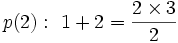
حال میدانیم لااقل برای تعدادی از ابتدای اعداد طبیعی  درست است. اکنون با فرض آنکه برای
درست است. اکنون با فرض آنکه برای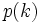 حکم درست باشد، درستی
حکم درست باشد، درستی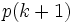 را نتیجه میگیریم (دقت کنید درستی
را نتیجه میگیریم (دقت کنید درستی 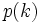 را فرض میکنیم.
را فرض میکنیم. 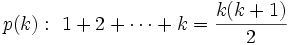

خوب حال شما بگوئید ما برای چند عدد طبیعی کوچکترین درستی را ثابت کرده و با فرض درستی
را ثابت کرده و با فرض درستی 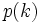 درستی
درستی 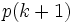 را ثابت کردیم، با این حساب آیا میتوان گفت که
را ثابت کردیم، با این حساب آیا میتوان گفت که برای تمامی اعداد طبیعی برقرار است؟ !
برای تمامی اعداد طبیعی برقرار است؟ !
به موضوع بالا فکر کنید چون اگر چه بعداً توضیح داده میشود ولی اگر اکنون آن را برای خود تجزیه و تحلیل کنید برای درک مطالب آینده راحتتر خواهید بود. چند نماد پرکاربرد
نماد مجموع  : از این جا به بعد با مجموع پشت سرهم دنبالهای از اعداد سروکار خواهیم داشت. برای نشان دادن مجموع
: از این جا به بعد با مجموع پشت سرهم دنبالهای از اعداد سروکار خواهیم داشت. برای نشان دادن مجموع  از نماد
از نماد 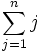 استفاده میکنیم، و این نماد یعنی تابع
استفاده میکنیم، و این نماد یعنی تابع 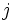 از حداقل مقدار 1 شروع شده و تا حداکثر
از حداقل مقدار 1 شروع شده و تا حداکثر  میرود و حاصل تمام مقادیر با هم جمع میشود. به طور کلی چند نمونه پرکاربرد:
میرود و حاصل تمام مقادیر با هم جمع میشود. به طور کلی چند نمونه پرکاربرد: 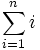 به جای
به جای 
 به جای
به جای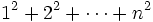
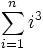 به جای
به جای 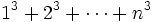
و به همین ترتیب …
و به طور کلی
از 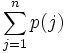 به جای
به جای 
استفاده میشود.
دقت کنید در نماد 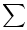 که آن را سیگما بخوانید سه قسمت مهم وجود دارد که در شکل قبل نشان داده شده است.
که آن را سیگما بخوانید سه قسمت مهم وجود دارد که در شکل قبل نشان داده شده است. قضیه .
میتوان سیگمای مجموع دو تابع یعنی 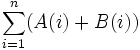 را به صورت مجموع دو سیگما هر یک از توابع یعنی
را به صورت مجموع دو سیگما هر یک از توابع یعنی 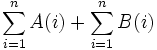 نوشت.
نوشت. قضیه .
 که k عددی ثابت است.
که k عددی ثابت است.
دو قضیه بالا به راحتی قابل اثبات بوده و از اثبات آنها صرفنظر میکنیم.
">نماد حاصلضرب
به طریق مشابه برای حاصلضرب 
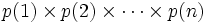 داریم:
داریم: 
به عنوان نمونه:  به جای
به جای 
 به جای
به جای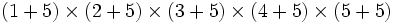 .
.
هانری پوانکاره
هانری پوانکاره ریاضی دان معروف فرانسوی است که در سال 1854 در خانواده ای به نام و سرشناس در شهر نانسی فرانسه به جهان قدم گذارد. از دوران کودکی فکرش سریعتر از کلمات کار می کرد در پنج سالگی به دیفتری مبتلا شد و در طی نه ماه حنجره اش از کار افتاد و همین مساله باعث گوشه گیری او شد به طوری که در بازیها نمی توانست شرکت کند. همین موضوع باعث شد که افکارش را متمرکز کند. او از حافظه بسیار خوبی برخوردار بود از شانزده سالگی شوق ریاضیات در پوانکاره بوجود آمد. او کارهای ریاضی را در ذهنش انجام میداد بدون اینکه آنها را یادداشت کند. پوانکاره مهمترین چهره در نظریه معادلات دیفرانسیل و ریاضیدانی است که بعد از اسحاق نیوتن مهمترین کار را در مکانیک آسمانی انجام داد در سال 1873 در راس هم دوره ایهای خود وارد مدرسه پلی تکینک شد استادش در نانسی به وی به عنوان غول ریاضی اشاره کرده است. پس از فارغ التحصیل شدن دوره های مهندسی را در مدرسه معادن ادامه داد و مدتی کوتاه به عنوان مهندس کار کرد واین کار مقارن زمانی بود که مشغول تهیه پایان نامه دکتری در ریاضیات بود این درجه را در سال 1879 گرفت. طولی نکشید که به تدریس در دانشگاه کان مشغول شد و در 1881 استاد دانشگاه پاریس شد و در آنجا تا زمان مرگ تدریس نمود در اوایل 33 سالگی به عضویت فرهنگستان علوم و در 1908 به عضویت فرهنگستان فرانسه انتخاب شد نیز به دریافت تمجیدها و افتخارهایی از فرانسه و کشورهای دیگر نایل آمد.
در سال 1880 در سن 26 سالگی درخشانترین اکتشافات را کرد و شهرت جهانی یافت و آن به سبب کشف دوران ساز تابع های خود ریخت از یک متغیر مختلط بود(خود وی آنها را تابع های فوکسی و کلاینی نیز نامید) و نظریه عمومی توابع را به هم ریخت دارای یک متغیر مختلط یکی از معدود شاخه های ریاضی است که وی تقریباٌ کاری برای پسینیان خود نگذاست اما نظریه توابع فوکس فقط یکی از خدمات متعددی است که او به نظریه توابع تحلیلی کرده است در مقاله کوتاهی که در سال 1883 تنظیم کرد اولین کسی بود که به پژوهش در پیوندهای میان نوعی تابع کامل( که بوسیله خواص تجزیه وایر شتراسی خود به عاملهای اول معین می شود) و ضرایب گسترش تیلری آن یا نرخ رشد مقدار مطلق تابع، پرداخت و از طریق تابع های مطلق به نظریه وسیع و کامل تابع های مرومورفی که هنوز بعد از 80 سال به نحو کامل فیصله نیافته است، رسید.
مهمترین سهم پوانکاره در هندسه جبری مقاله های 1910 تا 1911 او بود در باره منحنیهای جبری محتوی در یک سطح جبری پوانکاره یکی از شاگردان ارمیت بود و بعضی از کارهای آغازینش مربوط می شود به روش ارمیت در باره تحویل مداوم در نظریه حسابی صورتها و بخصوص قضیه متناهی بودن برای طبقه های اینگونه ضورتها که قبلاٌ ژوردان آن را اثبات کرده بود.
بررسی های پوانکاره در باره پیدایش جهان، آنالیز، نور و الکتریسیته و همچنین جبر و احتمالات بسیار مهم و دقیق است وی در فلسفه و علوم نظری صاحب نظر و محقق بود پوانکاره به کشف و حل مسائل بسیاری در ریاضیات نایل آمد که تا آن زمان به پی بردن آن ناتوان بودند کتابهای زیادی در زمینه های گوناگون علمی نوشت که بر جسه ترین آنها در ریاضیات و فلسفه عبارتند از: علم و فرض، علم و روشنی، مفروضات تکوینی، روشهای نوین در مکانیک آسمانی و ارزش علم تعداد کتابهای پوانکاره سی جلد می باشد و صاحب پانصد مقاله است که مربوط به مسائل کاملاٌ مختلف است با کشف توابع فوکس که پوانکاره به دنیای دانش تقدیم نمود برای حل معادلات دیفرانسیل که قبلاٌریاصیدان آلمانی لازار فوکس کشفیات زیبایی در مورد آنها کرده بود کلید جدیدی به کار برد و به کمک آن نه تنها مشکل معادلات دیفرانسیل را حل کرد بلکه معماری توابع بیضوی را نیزروشن ساخت اکتشافات وی در مبحثی از ریاضی که سابقاٌ آن را تحلیل تواضع می نامیدند و امروزه موسوم به توپولوژی جبری و از بزرگترین و مشکلترین مباحث ریاضی جدید است ارزش قاطع دارد همگی نظریه توابع فوکس از آغاز با اندیشه انتگرال گیریخطی معادله های دیفرانسیل با ضرایب جبری هدایت می شد اما رغبت بیشتر پوانکاره به نظریههای نور و موجهای برق مغناطیسی بود. نکته ای که وی در باره امکان ارتباط میان پرتوهای مجهول و پدیده شبتابی گفت آغازگر آزمایشهای هانری بکرل بود که وی را به کشف پرتوزایی رادیو اکتیویته کشانید از سوی دیگر پوانکاره از سال 1899 به بعد در بحثهای مربوط به نظریه الکترونی لورنتس بسیار فعال بود پوانکاره اولین کسی بود که دریافت که تبدیلهای لودنتس تشکیل گروهی می دهند که با گروهی که صورت درجه دوم را نامتغیر می کند هم ریخت است، بسیاری از فیزیکدانان بر این عقیده اند که در اختراع نظریه نسبیت خاص، پوانکاره با لورنتس و آلبرت انیشتین شریک است. انری پوانکاره در بهار 1912 مریض شد و 9 ژوئیه همان سال تحت عمل جراحی قرار گرفت و در 17 ژوئیه سال 1912 وقتی مشغول لباس پوشیدن بود در سن 68 سالگی در گذشت.
سایت رشد
